Definice.
Geometrickou řadou rozumíme libovolnou řadu ve tvaru
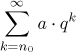
pro nějaké reálné konstanty a a q.
Zde ukážeme dva základní příklady řad - geometrickou řadu a p-řadu. Jsou dost důležité, protože mnohé testy konvergence tyto dva typy používají jako referenci. Na závěr se podíváme na alternující řady.
Geometrickou řadu dostaneme, když sečteme geometrickou posloupnost (viz Posloupnosti - Teorie - Úvod - Důležité příklady).
Definice.
Geometrickou řadou rozumíme libovolnou řadu ve tvaru
pro nějaké reálné konstanty a a q.
Toto je nejobecnější definice, ale mnozí lidé dávají přednost práci s řadami
ve tvaru
![]() .
Vlastně stačí znát jen tyto řady, protože libovolná řada z naší definice se
na tuto jednodušší dá snadno převést. Konstanta a se dá vytknout z
řady, takže její chování neovlivní, a nakonec ji
zase můžeme zahrnout do výsledku, který dostaneme bez ní. Druhý problém k
vyřešení je změnit indexaci tak, aby začala v 0. To se dá udělat vytknutím
nejmenší mocniny z řady a pak přeindexováním substitucí.
.
Vlastně stačí znát jen tyto řady, protože libovolná řada z naší definice se
na tuto jednodušší dá snadno převést. Konstanta a se dá vytknout z
řady, takže její chování neovlivní, a nakonec ji
zase můžeme zahrnout do výsledku, který dostaneme bez ní. Druhý problém k
vyřešení je změnit indexaci tak, aby začala v 0. To se dá udělat vytknutím
nejmenší mocniny z řady a pak přeindexováním substitucí.
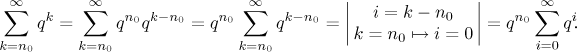
Proč to funguje uvidíme lépe, když si řadu rozepíšeme dlouhým způsobem, pak je to vlastně jasné.
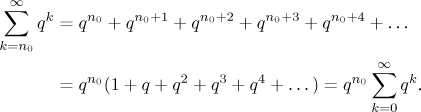
Jak vidíme, tento vytýkací trik závisí silně na tom, že členy této řady jsou mocniny se shodným základem, jinými slovy, nebude fungovat u jiných řad než geometrických (či jim velmi podobných). Ale zpět k tématu: Protože se ona obecnější forma snadno převede na tu jednodušší a je to nuda ji psát, nadále budeme vždy pracovat s tou přátelštější, jednodušší formou geometrické řady.
Geometrická řada je velmi populární, protože o ní všechno víme. Všimněte si,
že všechny příklady v první sekci (viz
Úvod) byly geometrické řady.
Volba ![]() ,
volba
,
volba ![]() a volba
a volba
![]() .
No a volba
.
No a volba ![]() .
Co se tedy dá říct o geometrické řadě? Za prvé, pomocí matematické indukce
hravě dokážeme, že pro částečné součty máme následující vzorce (pro
q různé od 1):
.
Co se tedy dá říct o geometrické řadě? Za prvé, pomocí matematické indukce
hravě dokážeme, že pro částečné součty máme následující vzorce (pro
q různé od 1):
![]()
Pro q = 1 máme
Fakt.
Uvažujme geometrickou řaduTato řada konverguje pro .
|q| < 1 a diverguje pro|q| ≥ 1. Navíc
Už jsme ukázali, že stačí znát vzorce pro řadu, jejíž index začíná v 0, ale někteří lidé neradi blbnou s algebrou a raději si pamatují obecnější vzorce.
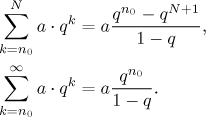
Je šest základních typů geometrických řad, odpovídají typům popsaným v sekci Důležité příklady v části Posloupnosti - Teorie - Limita.
V této části budeme uvažovat řady typu
![]() , kde p
je parametr. Hned se naskýtá otázka, proč píšeme řadu takto, se členy jako
zlomky; proč ony členy nenapíšeme jednodušeji jako
kq? Důvodem je, že chceme mít
, kde p
je parametr. Hned se naskýtá otázka, proč píšeme řadu takto, se členy jako
zlomky; proč ony členy nenapíšeme jednodušeji jako
kq? Důvodem je, že chceme mít
Když se totiž podíváme na p-řadu (ve tvaru napsaném výše) a zeptáme
se, co se stane s jejími členy pro
Co se děje, když uvažujeme kladné p? Všimněte si, že když zvyšujeme
p, tak se čísla
Fakt ( p-test).
Jestliže p > 1, pak řadakonverguje.
Jestliže p ≤ 1, pak.
Důkaz tohoto extrémně užitečného
Příklad:
Uvažujme řadu
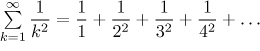 .
.
p-test říká, že tato řada konverguje
V příští sekci budeme mluvit o tom, jak je těžké sečíst řadu. Tato řada není žádnou výjimkou, dá to docela dost práce ukázat, že ve skutečnosti
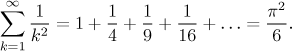
Protože jsou všechny členy této řady kladné, tak automaticky konverguje absolutně a tudíž máme konvegenci pro všechny modifikace znamének. Když tedy například změníme tuto řadu v řadu alternující, dostaneme konvergenci a další zajímavý výsledek.
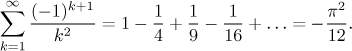
Bonus: Elementární důkaz, že řada čísel
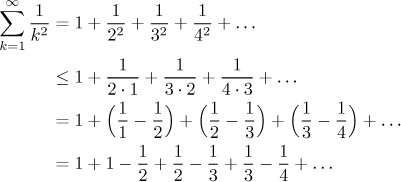
Teď se zdá, že by řada měla konvergovat a součet by neměl překročit 2. Je tomu opravdu tak, rigorózní důkaz lze dostat mírným dopracováním našeho odhadu (viz teleskopická řada v následující sekci a srovnávací kritéria v části Teorie - Testování konvergence).
Příklad:
Uvažujme řadu
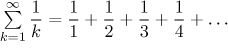 .
.
p-test říká, že tato řada diverguje
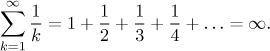
Částečným součtům harmonické řady se říká harmonická čísla a značí se Hn. Jejich přesné hodnoty nejsou známy, přestože už do jejich zkoumání bylo investováno dost výzkumu. Harmonická řada je docela zajímavá, protože když z ní uděláme alternující řadu, stane se konvergentní, viz Leibnizovo kritérium (v části Teorie - Testování konvergence). Dokonce víme, jaký je její součet (viz příští sekce),
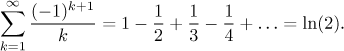
Tato alternující řada konverguje, ale když její členy zavřeme do absolutní hodnoty, dostaneme divergující harmonickou řadu. Je to tedy ukázkový příklad neabsolutně konvergentní řady.
Bonus: Elementární důkaz divergence harmonické řady. Tento důkaz je prý jedním z vrcholů středověké matematiky.
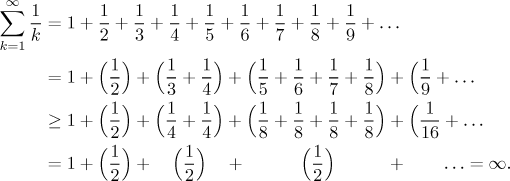
Viz také tato poznámka.
Poznámka:
Máme teď pěknou příležitost zdůraznit jeden klíčový rozdíl. Když máme
hromadu čísel ak, můžeme z nich vyrobit dva různé
objekty, posloupnost a řadu. Tyto dva nemusí mít stejné vlastnosti.
Například čísla
Poznámka týkající se vybraných řad: Všimněte si, že řada v prvním
příkladě (ta s
Trochu více překvapivý je fakt, že to také může fungovat naopak. Víme například, že alternující harmonická řada konverguje. Když z ní ale vytáhneme každý druhý člen, dostaneme divergentní řadu
![]()
Důkaz její konvergence je snadný pomocí limitního srovnání.
Jménem alternující řada označíme libovolnou řadu, u jejichž členů se
pravidelně střídají znaménka, tedy znaménka jdou
Všimněte si, že někdy máme přirozené vyjádření řady, které má
Alternující řady se objevují docela často a (relativně) snadno se s nimi pracuje, viz ono už zmíněné Leibnizovo kritérium či poslední Fakt v sekci Aproximace řad v části Teorie - Úvod do řad.