Bisection method and Newton method

Consider the following problem. We have a function f and we want to find some point at which the value of f is a given number. We will show two methods. The bisection method is more general, it looks for points that satisfy some property (not necessarily related to a value of some function, but this is the most natural setting for it). On the other hand, the Newton method addresses a special case of the "value problem", namely it searches for a point where the given function is zero.

Bisection method

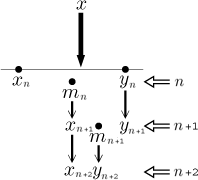
This method is used in many situations to find a number with a certain property. It actually uses two sequences, not just one, and the reason will be clear right away. The idea of bisection is this: We somehow find (for instance by guessing) two numbers x_n < y_n so that the desired number lies between them. Then we take their middle m_n = (x_n + y_n)/2. If this middle is the number, we are done. If not, then since it was in the interval (x_n, y_n) to start with, it must necessarily be in one of the smaller intervals created by splitting the original one into halves, that is, either between x_n and m_n, or between m_n and y_n. Whichever the case, we take the appropriate couple as the next starting couple with index n +1. The picture shows two steps of a typical search for the number x.

Since at every step, the terms of the two sequences that thus arise are half of the previous distance, they eventually corner the desired number with arbitrary precision.

Now we show how to apply this idea to finding the square root of a given positive number A.
We start by guessing two positive numbers x₀ < y₀ such that x₀² < A < y₀². This means that the desired square root must be somewhere between these two numbers.
Now we define the general recursive step. Given a couple x_n < y_n such that x_n² < A < y_n², we find the middle m_n = (x_n + y_n)/2. If we are lucky, we get the square root. If not, then the square root must either be between x_n and m_n (if x_n² < A < m_n²), or it must be between m_n and y_n. Whichever the case, we pick the appropriate numbers as the new couple x_n+1 and y_n+1 and the procedure continues. As an example we show how to find the square root of 19.3.

We will show how the bisection method is used to find roots of functions in the next part. The bisection method is generally slow in getting the necessary precision (in every step we only halve the possible error), but it is quite reliable; all we need is to find some bounds for the desired number to start the procedure and the method works. Note that the method used for finding the square root explained below reduces the error much faster.

The last remark concerns the choice of the middle. There exists a modification of the bisection algorithm that works faster by choosing not the middle, but a point expected to work well. Given x_n and y_n, we at some point test them how close they get to satisfy some requirement, in our example how close their square is to A. It is natural to expect that if, for instance, y_n² is much closer to A than x_n², then the real square root of A will be closer to y_n than to x_n. So instead of trying the middle m_n in our next step, we would test a number which is somewhat closer to y_n. The precise choice is usually done proportionally, comparing on how close the numbers y_n and x_n are to the desired property.

One of the frequently asked problems in analysis is to find some root of a given function. That is, given formula for f (x), we want to find a number r such that f (r) = 0 (if such a number exists). For quadratic polynomials this is easy using the well-known formula, but the formulas for the roots of cubic polynomial are nasty and for polynomials of degree 4 and more there is no formula at all. Functions other than polynomials are even worse. For instance, can you find x such that e^x + x = 0? This is actually quite typical of mathematics, problems that are very simple to state may turn out to be very difficult.

One possibility is to apply the bisection method above. It would go like this:

Assume that we have a function f (x), we want to identify a number r so that f (r) = 0. Assume further that we have numbers x₀ < y₀ such that f (x₀) and f (y₀) have different signs (if one of these two is zero, we found the root and the procedure ended). Then it is reasonable to expect that the desired root is somewhere between these two, for continuous functions it it surely true (see the Intermediate value theorem in Functions - Theory - Real functions - Continuity).

We define the sequences {x_n} and {y_n} in the following way:

Given x_n and y_n such that f (x_n) and f (y_n) have different signs, consider the middle m_n = (x_n + y_n)/2.

If f (m_n) = 0, we found the root and the procedure ends.
If f (x_n) and f (m_n) have different signs, we set x_n+1 = x_n and y_n+1 = m_n.
If f (m_n) and f (y_n) have different signs, we set x_n+1 = m_n and y_n+1 = y_n.

Note that if f has different signs at x_n and y_n and f (m_n) is not zero, then one of the above alternatives must happen, one of the new couples must give different signs in f, the root is then between them (hopefully).

As we remarked above, this method is reliable but rather slow. One of the most popular tools for finding a root is the Newton method. It assumes that the given function has a derivative.

Newton method.
Pick some starting value x₀. We define recursively
(1) x_n+1 = x_n − f (x_n)/f ′(x_n), n = 0,1,2,3,...

If this sequence converges, then its limit r satisfies f (r) = 0.

How did we get this formula? It is actually quite simple using elementary geometry, if you are curious, click here. You will also find a simple example there of the method failing, which can easily happen. That is the disadvantage of the Newton method. On the other hand, if it works, it is very fast in yielding the required precision. In the next part we will show one useful application.

You have a positive real number A. How do you find the square root of it? Of course, unless you are really lucky, the answer will not be an integer. So with this question also comes another important piece of information: How precise the answer should be.

Note that in mathematics you can give an absolutely precise answer. You draw that funny gallows sign over the A and say: Here's your root. And indeed, that is the correct answer. However, in the real world (and in mathematics when it gets applied) you need to know the answer in the decimal form. The purpose for which you need this root will also determine the required precision. If you just want to mark it on your ruler, it is pointless to ask for more than two decimals, the point of your pencil is thicker than this anyway. On the other hand, you may be using it in some involved calculation (for instance in engineering) where five decimals might be needed. You may even be the manufacturer of calculators, in which case you would want to know the answer with the precision of, say, 13 digits.

So here we go again, how do you find the root of A? There is a "paper and pencil" algorithm for finding the root that you probably learned in elementary school (and forgot since), but it is not exactly convenient for computers. We will try to use the Newton method using a trick: We will look for a root of the function f (x) = A − x². We see that the square root of A is the positive root of f. What happens if we apply the Newton method to the square root problem in this setting? We will get an interesting sequence.

We define recursively
(0)    a₀ = A (or some other value, it's not really important),
(1)    a_n+1 = 1/2(a_n + A/a_n), n = 0,1,2,3,...

It can be proved that such a sequence is convergent, and the limit is exactly the square root of A (similar sequences exist also for other roots). This algorithm is easy to program into a computer or a calculator and it finds the root quite quickly.

For instance, my calculator says that the square root of 2 is approximately 1.4142136. We try the sequence:
a₀ = 2, a₁ = 1.5, a₂ = 1.4166667, a₃ = 1.4142157, a₄ = 1.4142136.
As you can see, it works quite well. It can be proved that every iteration of this procedure approximately doubles the number of decimal digits that are correct.

Back to Theory - Applications