We first introduce continuity at a point, then explore its properties and discontinuities. Next two parts cover continuity on a set and properties of continuous functions on intervals.
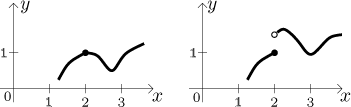
In the Example introducing functions we at one point used the fact that the car moves through all intermediate stages, that is, it cannot jump instantaneously from one place to another. This is called continuity. When you look at the following two graphs, you should see one basic difference. While you can draw the first graph without lifting your pencil off the paper, in the second graph you have to make a little jump.

This difference may have far reaching consequences. Now we need to somehow
express the idea of "connectedness" formally; unfortunately, there are much
worse functions than the one on the right out there, so we have to get a bit
technical and start by investigating situation at a given point. To be
continuous at a given point a means roughly the following. The
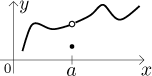
function must be defined at that point, so we have a dot in the graph of
f representing the value
Consider the example above and the point
We therefore compare two things, the value of f directly at a and the behaviour of f around a, but we already have a name for it, this is called limit. For uninterrupted graph at a we want these two different kinds of information (at a point, around this point) to agree.
Definition.
Let f be a function defined on some neighborhood of a point a. We say that the function f is continuous at a if the limit of f at a converges tof (a).
Before we get further in investigating continuity, note that when we are approaching the given point, we have a choice between aproaching from the right and from the left. For continuity we need to consider both approaches. However, sometimes we are interested only in one side. This might make sense. For instance, in the second example above, if we ignore parts to the right of 2 then the graph is "better", without jumps.
The definition of one-sided continuities is almost like the one above, we just have to restrict those x to an appropriate side of a.
Definition.
Let f be a function defined on some left neighborhood of a point a. We say that the function f is continuous from the left at a if the limit of f at a from the left converges tof (a).
Let f be a function defined on some right neighborhood of a point a. We say that the function f is continuous from the right at a if the limit of f at a from the right converges tof (a).
Mathematically we express continuity and one-sided continuity with the following three equalities:
![]()
If we use the shortcut for one-sided limit, continuity from the left and right can be also expressed like this:
Note that some authors define continuity in a different way, but at the
end it comes up to the same notion. Thinking about this other definition
might be very useful for those who are trying to understand analysis well,
we offer it
here.
You may look
here
for an advanced technical remark.
The following theorem should be no surprise if you have the proper idea of what continuity means.
Theorem.
A function f is continuous at some point a if and only if it is continuous at a both from the left and right.
We start with discontinuities.
Definition.
Let f be a function defined on some neighborhood of a point a. We say that a is a point of discontinuity of f if f is not continuous at a.
We can classify discontinuities according to how badly continuity fails, that is, how much we fail with the following equality:
![]()
There are more things that can go wrong there, we start from the least problem.
Classification of discontinuities:
1. Removable discontinuity.
We say that a function f has a removable discontinuity at a
point a if it has a proper limit at a, but this limit is not
equal to
This is the nicest case, we have almost everything than is needed for continuity, just a little problem there. Here is a typical example:
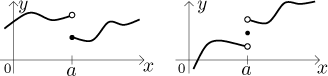
Now you can see why it is called removable discontinuity. It is enough to change the definition of f at just one point, namely at a, and the new function will be continuous. Precisely, defining
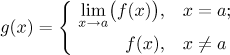
we get a function that is continuous at a. Intuitively, we simply move the point in the graph to fill in the hole.
2. Jump discontinuity.
We say that a function f has a jump discontinuity at a
point a if it has proper one-sided limits at a, but they are
not equal.
When the one-sided limits are not equal, then the limit as such does not exist. So this is a case that is a bit worse than the removable discontinuity, but the existence of one-sided limits still makes this a nice case. Here are two typical examples of jumps, the one on the left is at least continuous at a from the right:
Now you can see why it is called a jump discontinuity. If we wanted to fix the discontinuity now, it would not be enough to change just one point. To "connect" the function at a, one would have to shift half of the function up or down.
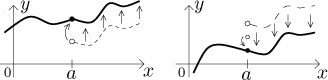
So this is not as nice as the removable discontinuity, but one can still get a continuous function out of it.
3. Discontinuity of the third kind.
We say that a function f has a discontinuity of the third
kind at a point a if it does not have one or both one-sided proper
limits at a.
Here we lump all other cases. They have one thing in common, the function cannot be fixed to be continuous at a by merely shifting a part of it. Some typical cases are in the picture:
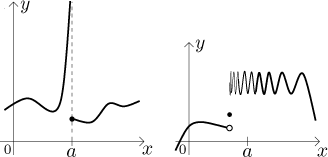
In the first picture, there are one-sided limits, but one of them is improper. Obviously, one cannot shift the right part to connect the graph. Still, this is actually a rather nice case, since there are definite tendencies and we have useful information. We will return to such cases when talking about asymptotes.
In the second picture, the limit from the right does not exist, not even improper, so this is even worse.
Continuity and operations.
Theorem.
Let f,g be functions continuous at a point a. Then the functionsf + g, f − g, andf⋅g are continuous at a. Ifg(a) ≠ 0, then also the functionf /g is continuous at a.Let f be a function continuous at a point a, let g be a function continuous at the point
f (a). Then the composed functionf ○ g is continuous at a.
Example.
Before we move further, we should clarify some misconceptions. The above
pictures were in fact too nice in one aspect. In order to draw functions
properly, we made them nice around the point a. However, continuity at
a only gives us information about that particular point and about
tendencies toward it, not anything else. Consider therefore the following
function.
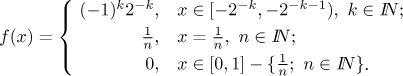
How does it look like? First we look at the negative part, interval
On the interval
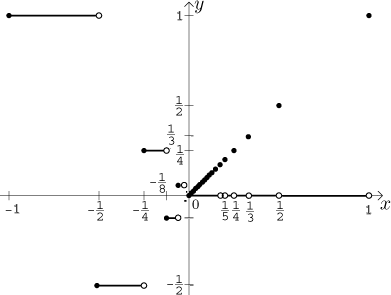
Since for every x we have
For another example of a weird yet continuous function see "Saw-like" functions in Theory - Elementary functions. If you did not have enough, in Dirichlet function there is a weird function that is continuosu at 0 but it does not even have any uninterrupted part in its graph.
Definition.
Let f be a function, let M be a subset of the domain of f. We say that the function f is continuous on M if it is continuous at every point of M when considered as a function restricted to M.
This is a nice definition that is used in general, but for practical use with real functions it is not the best one. We will now therefore make a special definition for a special type of a set: an interval.
Definition.
Let f be a function defined on a non-degenerate interval I. We say that the function f is continuous on the interval I if it is continuous at every interior point of I and also at those endpoints that belong to I from the appropriate side.
For instance, consider a function f on an
interval
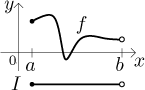
This definition applies also to infinite intervals, with infinity as one or both endpoints. Now when we say that a function is continuous on a set, then if this set is a non-degenerate interval, we will use this new definition. If this set is a union of non-degenerate intervals, then continuity on this set means continuity on each of these intervals by the new definition. Only if we have some other set then we will use the first definition, but we meet such sets only rarely.
We will make still another definition so that we can quickly say that a function is the best possible from the point of view of continuity.
Definition.
Let f be a function. We say that it is continuous if it is continuous on its domain.
Finally we are getting to the interesting part. The above example of a function continuous at 0 showed that knowing continuity at some point does not really make this function "nice", we were in fact even unable to draw that function properly, since it had infinitely many jumps as it approached 0 from the left and also from the right. However, once we know that a function is continuous on an interval, we know that we can draw it as a uninterrupted curve on that interval. This still does not guarantee that the function will be nice and can be drawn properly (see for instance the "Saw-like" functions in Theory - Elementary functions), but functions continuous on intervals are better than most.
Theorem (continuity and operations).
Let f,g be functions continuous on a set M. Then the functionsf + g, f − g, andf⋅g are continuous on M. The functionf /g is continuous on the setM − {x; g(x) = 0}. Let f be a function continuous on a set M, let g be a function continuous on the set
f (M). Then the composed functionf ○ g is continuous on M.
We mentioned that functions are often investigated on each interval of their
domain separately and then the information is put together. How does it work
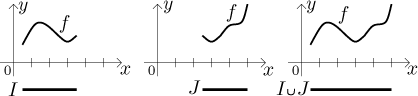
for continuity? Consider the following situation: We have a function f
and we know that it is continuous on an interval I and on an interval
J. What can we say about continuity on the set
If the two intervals overlap (that is, if their intersection is not empty), then they have at least one common point. Since this point is common to both pieces of the graph, it forces the two pieces to join nicely, therefore the function is again continuous on the union.
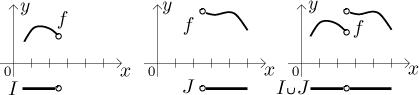
If the intervals are disjoint and not adjacent, then the function is always continuous on their union M as well. Why? If the intervals have no points in common, then the two corresponding (nice uninterrupted) pieces of graph are not positioned one next to another, and therefore nothing bad can happen when we look at these two pieces as a whole. Similar conclusion applies to the case when the intervals are adjacent, that is, they share one common endpoint, but they are both open at that endpoint. This point then does not belong to any of them, hence it is not a part of their union and therefore it separates the two pieces of graph. Consequently, we do not have to worry about continuity there.
The third case is the only "interesting" one, since here we have to do some work. The only case not covered by the above two alternatives is when the two intervals meet, that is, they have a common endpoint, call it c, and this endpoint belongs to exactly one of those intervals. This point then also belongs to the union M, and since it was the meeting point of the two intervals, it will actually belong to the interior of M. Thus the graph of f is defined both to the left and the right of c and we have to worry whether these two pieces connect well or not. It is therefore necessary to consider one-sided limits at c. If they agree, the pieces of function connect well and the function is continuous on M, otherwise it has some kind of discontinuity at c (it need not be jump discontinuity, as a function continuous on an open interval need not have one-sided limits at its endpoints).
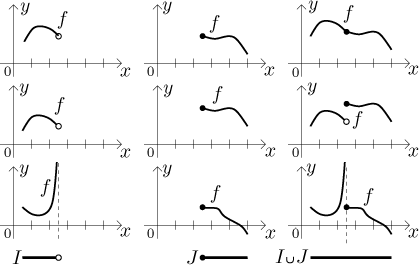
These considerations come in handy especially when exploring continuity of functions defined by cases, since then we are putting together parts of functions considered on different sets, these sets would typically connect in exactly the way we looked at in the third alternative.
When working with a function, we sometimes worry about it being zero. As an
example, consider the fraction
Therefore we often we require more, we want f to be separated
from zero. This means that there is a certain strip around 0 into which
f does not enter. Expressed using inequalities this means that there
is a certain constant
Continuity offers a chance to get this separation at least locally.
Theorem.
Assume that a function f satisfiesf (a) ≠ 0. If f is continuous at a, then there exists a neighborhood U of a and a constantk > 0 such that| f | > k on U.
Note that without continuity the conclusion need not be true. In fact,
without continuity we do not have even a weaker statement that
Now we pass to properties of functions continuous on intervals. We start with a definition:
Definition.
We say that a function f satisfies the Intermediate Value Property (IVP) on a set M if for any two points x,y from M and any value d between the numbersf (x), f ( y) there is a number c in M such thatf (c) = d.
In short, for every two values that a function with IVP attains, it must also attain all values between. A picture suggests the meaning of the above definition.
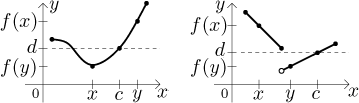
The first situation is "typical", that is, "nice". The second example also satisfies the IVP, but note that it does so in a rather unexpected manner. The point c that we find for the indicated d does not lie between x and y! This is perfectly all right, the definition did not require any special placement of c, just its existence. Try different choices of x,y and different values of d in this second example to convince yourself that this function indeed satisfies IVP. However, just a little change in the function will result in another function that fails IVP:
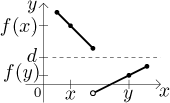
Try to think of other functions that fail IVP. If you do it, you should start having a feeling that the failure of IVP somehow relates to the fact that there must be jumps in the function. As we saw, not every function with jumps fails IVP, but not having them actually guarantees IVP assuming that the set M is an interval (including an infinite one).
Theorem (Intermediate Value Theorem, IVT).
Every function continuous on an interval satisfies the Intermediate Value Property on that interval.
For another result concerning IVP see derivative as a function in Derivative - Theory - Introduction - Derivative and basic properties.
Corollary.
Let f be a function continuous on an interval[a,b]. If the valuesf (a), f (b) have opposite signs, then some root of f exists somewhere in the interval(a,b).
This statement is the theoretical basis for the popular bisection method for finding roots, see Bisection method in Sequences - Theory - Applications. It is also helpful in situations when we want to determine the sign of some function. The corollary says that for a continuous function to change from negative to positive or vice versa, it must cross the x-axis. This can be restated as follows: If such a function does not have a root somewhere, then it cannot change its sign there.
Corollary.
Let f be a function continuous on an interval I. Let a,b be two neighboring zero points of f from this interval, that is, there are no other zero points of f between a and b. Then either f is always positive on(a,b) or f is always negative on(a,b).
This is the basis for yet another popular method. When investigating signs of some expression, we often start by finding the zero points of this expression. These become the breaking points where the sign could change and split the real line into intervals of constant sign. For a certain interval, the appropriate sign can be determined simply by substituting some point from this region into the given expression.
In the previous section we defined supremum, infimimum, minimum and maximum and we remarked that the maximum and minimum need not exist even for bounded functions on a closed interval. However, we have the following fact.
Theorem (Extreme value theorem, EVT).
Every function continuous on a bounded closed interval attains its maximum and minimum over this interval.
In particular, a continuous function on a bounded closed interval must be bounded.
The theorems IVT and EVT combine to this statement:
If f is a continuous function on a bounded closed interval I, then it maps I onto a bounded closed interval.
We know that a strictly monotone function on an interval must be 1-1, therefore it has an inverse there. If the function is continuous, this implication becomes an equivalence; moreover, the inverse function is also nice.
Theorem.
Let f be a function continuous on an interval I. Then f is 1-1 on I if and only if it is strictly monotone on I. If it is so, then the corresponding inverse function to f is also continuous on its domain.
Monotonicity of real functions
Back to Theory - Real
functions