Intervaly a okolí, rozšířená reálná osa

V této sekci uvedeme základní nástroje pro práci na reálné ose a rozšířenou reálnou osu.

V analýze často mluvíme o tom, že je něco blízko. Když mluvíme o blízkosti, tak je klíčovým pojmem vzdálenost. Na reálné ose používáme tu obvyklou, kdy je vzdálenost mezi body a a b dána výrazem |a − b|. Všimněte si, že nerovnost |a − b| > 0 je ekvivalentní tomu, že se a a b nerovnají. To se použije za chvíli.

Definice.
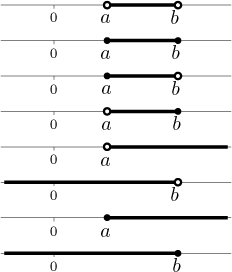
Uvažujme reálná čísla a < b. Definujeme
otevřený interval     (a,b) = {x∈ℝ; a < x < b},
uzavřený interval     ⟨a,b⟩ = {x∈ℝ; a ≤ x ≤ b},
polouzavřený interval (nebo polootevřený interval)     ⟨a,b) = {x∈ℝ; a ≤ x < b},
polouzavřený interval (nebo polootevřený interval)     (a,b⟩ = {x∈ℝ; a < x ≤ b}.

Definujeme také
otevřený interval     (a,∞) = {x∈ℝ; a < x},
otevřený interval     (−∞,b) = {x∈ℝ; x < b},
uzavřený interval     ⟨a,∞) = {x∈ℝ; a ≤ x},
uzavřený interval     (−∞,b⟩ = {x∈ℝ; x ≤ b},

Bodům a, b říkáme krajní body těchto intervalů, mluvíme o intervalech od a do b. V posledních čtyřech případech považujeme také nekonečno a mínus nekonečno za krajní bod.

Abychom měli lepší představu o vlastnostech množin a bodů, kreslíme si je na reálné ose. U intervalů používáme plné tečky pro uzavřené krajní body a prázdná kolečka pro otevřené krajní body. Ve stejném pořadí jako v definici:

Intervaly jsou velice populární, protože mají mnoho užitečných vlastností. Asi nejdůležitější vlastnost je to, že jsou to souvislé množiny, což znamená, že když máme dva body z intervalu I, pak umíme přejít od jednoho k druhému, aniž bychom se dostali ven z I. Platí, že každá souvislá podmnožina reálných čísel je interval. V další části uvidíme, kde se vzalo to otevřené/uzavřené názvosloví. Uvidíme také, že intervaly s nekonečny nejsou nijak speciální, ale na to budeme muset rozšířit reálnou osu. Mimochodem, když už mluvíme o nekonečnech, množina reálných čísel je také interval, jmenovitě (−∞,∞).

Jsou dva druhy poněkud srandovních intervalů, které nejsou u mnoha aplikací zrovna vítány, jmenovitě pro libovolné a máme (a,a) = {} a ⟨a,a⟩ = {a}. Analogické polouzavřené intervaly jsou také prázdné. Tyto prázdné a jednobodové intervaly se nazývají degenerované, všechny ostatní intervaly jsou nedegenerované. V mnoha aplikacích chceme pracovat jen s nedegenerovanými intervaly, protože ty mají neprázdný vnitřek (viz další sekce).

Intervaly jsou důležité, protože mnoho metod, které budeme používat, funguje jen na intervalech, jsou tedy v jistém smyslu naším pracovištěm. Teď uvedeme jiný typ množin, které budou v analýze naším pracovním nástrojem.

Rozdíl je v tom, že okolí obsahuje svůj referenční bod a, zatímco prstencové okolí ne. Tato okolí je také možno vyjádřit pomocí intervalů, například

U_ε(a) = (a − ε,a + ε);       P_ε(a) = (a − ε,a) ∪ (a,a + ε).

Okolí používáme k vyjádření některých důležitých myšlenek. V mnoha situacích totiž potřebujeme vědět, co se děje bezprostředně vedle daného bodu, a to se nejlépe vyjádří pomocí okolí, jak uvidíme níže. Někdy je nám jedno, co se děje na obou stranách a, zajímá nás jen jedna strana. Na to používáme jednostranná okolí.

Definice.
Uvažujme reálné číslo a a nějaké ε > 0.
Definujeme pravé ε-okolí bodu a jako

U_ε⁺(a) = ⟨a,a + ε).

Definujeme levé ε-okolí bodu a jako

U_ε^-(a) = (a − ε,a⟩.

Definujeme pravé prstencové ε-okolí bodu a jako

P_ε⁺(a) = (a,a + ε).

Definujeme levé prstencové ε-okolí bodu a jako

P_ε^-(a) = (a − ε,a).

Například levé okolí vypadá takto:

V některých situacích se vyplatí zacházet s nekonečnem jako s nějakým obyčejným objektem. Například když se ptáme na limitu v nějakém konkrétním bodě a a na limitu v nekonečnu, tak se ukáže, že postup použitý při zodpovězení takových otázek je v zásadě stejný. Ušetříme tedy čas, když mluvíme o nějakém a, které může být reálné číslo, ale také nekonečno či mínus nekonečno coby dva "konce" reálné osy.

Proto teď zavedeme rozšířenou reálnou osu (značeno ℝ^*) jako reálnou osu plus dva abstraktní prvky ∞ a −∞. Body této množiny spadají do dvou kategorií, reálná čísla jsou vlastní body a ony dva prvky ±∞ jsou nevlastní body.

Abychom mohli s rozšířenými reálnými čísly pracovat, musíme rozšířit také operace a uspořádání. Definujeme, že pro každé reálné číslo a máme −∞ < a < ∞. Položíme také |−∞| = ∞. Co se týče operací, tam je situace trochu delikátní. Musíme je definovat takovým způsobem, aby měly smysl a dobře zapadly k těm operacím, které už máme. Přirozeně tak přijdeme k následujícímu:

• Sčítání: ∞ + ∞ = ∞, ∞ + a = ∞ pro každé reálné a, ∞ − a = ∞ pro každé reálné a, −∞ + a = −∞ pro každé reálné a, −∞ − a = −∞ pro každé reálné a.
• Násobení: ∞ ⋅ ∞ = ∞, ∞ ⋅ a = ∞ pro každé reálné a > 0 and ∞ ⋅ a = −∞ pro každé reálné a < 0, −∞ ⋅ a = −∞ pro každé reálné a > 0 a −∞ ⋅ a = ∞ pro každé reálné a < 0, ∞ / a = ∞ pro každé reálné a > 0 a ∞ / a = −∞ pro každé reálné a < 0, −∞ / a = −∞ pro každé reálné a > 0 a −∞ / a = ∞ pro každé reálné a < 0. Definujeme také −∞ = (−1) ⋅ ∞.
• ∞^a = ∞ pro každé a > 0, ∞^a = 0 pro každé a < 0, a^∞ = ∞ pro každé reálné a > 1, a^∞ = 0 pro každé a splňujicí |a| < 1.

Všimněte si, že některé operace nejsou vypsány, například ∞ − ∞, 0 ⋅ ∞, ∞ / ∞, 1^∞ atd. Tyto operace nelze definovat tak, aby to mělo smysl, což lze vidět, když pracujeme s limitami (podívejte se například na poznámku o neurčitých výrazech).

Abychom využili výhody reálných čísel, musíme nejprve ještě zobecnit pojmy, které jsme měli výše. Za prvé, všimněte si, že v definici intervalů jsme vypsali čtyři zvláštní případy s nekonečnými krajními body, ale když teď máme rozšířenou reálnou osu, tak už je nepotřebujeme. Můžeme totiž prostě použít příslušné definice mezi prvními čtyřmi a aplikovat je také na případy, kdy jeden nebo oba krajní body jsou nekonečné. Poznamenejme, že nekonečna nikdy nejsou prvky intervalu (intervaly obsahují pouze reálná čísla), jinými slovy intervaly nikdy neuzavíráme v jejich nevlastních krajních bodech.

Další důležitý pojem je okolí a tady bude třeba trochu víc práce. Co od okolí očekáváme? Jsou to množiny, které jsou souvislé a jdou doleva a doprava od daného bodu a. U nekonečen toto není možné, protože je možné jít jen na jednu stranu, takže tam budeme muset udělat modifikaci. Pro nevlastní body tak pojmy jednostranného a oboustranného okolí vyjdou nastejno, nemáme moc na výběr. Také rozlišení mezi okolím a prstencovým okolím se ztrácí, protože okolí nekonečna (či mínus nekonečna) bude obsahovat pouze reálná čísla a tudíž bude automaticky prstencové.

Za druhé, okolí vlastního bodu je dáno parametrem ε, který říká, jak daleko můžeme zajít od daného bodu. Tohle nám nepomůže pro a nevlastní, protože každé reálné číslo je nekonečně daleko od nekonečna. Použijeme tedy jiný pohled na okolí vlastních bodů. Pokud vezmeme všechna možná okolí vlastního bodu a a necháme jít ε k nule (zprava, protože ε může být jenom kladné), pak konce těchto okolí jdou ke středu a. To už je něco, co dokážeme emulovat pro okolí nekonečna a mínus nekonečna. Teď už bychom měli být schopni porozumět následující definici.

Definice.
Uvažujme ε > 0.
Definujeme ε-okolí bodu ∞ jako

U_ε(∞) = (1/ε,∞).

Definujeme ε-okolí bodu −∞ jako

U_ε(−∞) = (−∞,−1/ε).

Teď už můžeme pracovat s okolími, aniž by nás zajímalo, zda je referenční bod a vlastní nebo nevlastní.

V situaci, kdy můžeme použít nekonečno jako bod, se mnoho definic, které by se musely dělat dvakrát, zúží na jednu. Pro jednoduchý příklad se podívejte na definici suprema na konci další sekce, velké zjednodušení je vidět v definici limity, viz Definice limity v části Funkce - Teorie - Limita funce.

Topologické pojmy
Zpět na Teorie - Reálná čísla