V této sekci se podíváme blíže na rozličné vlastnosti reálných čísel. Většina z nich má něco do činění s tím, co se děje blízko či daleko od určitého bodu, a věci tohoto typu se v matematice studují pod názvem topologie. Pak se podíváme na množiny a uspořádání.
Jedna z nejdůležitějších vlastností reálné osy je to, že "nemá díry" (viz Reálná čísla v sekci Extra - Množiny a zobrazení - Důležité číselné množiny). Začneme s jedním možným vyjádřením tohoto faktu.
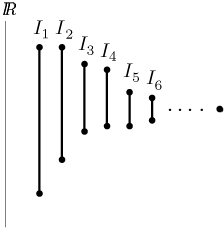
Intervalů se týká jedna důležitá vlastnost.Věta (Princip vnořených intervalů)
Nechť Ik pro přirozená čísla k jsou uzavřené intervaly reálných čísel. Pokud jsou tyto intervaly vnořené, tedy jestliže pro všechna k platíIk+1 ⊆ Ik, pak je průnik všech Ik neprázdný.
Pokud navíc délky těchto intervalů jdou do nuly, pak je jejich průnikem jediný bod.

Pronikání nekonečně mnoha intervalů je často zrádné, tento princip ukazuje,
že alespoň v případě vložených uzavřených intervalů se nemusíme bát.
Poznamenejme, že uzavřenost těchto intervalů je zde zásadní, jinak by průnik
mohl být prázdný. Například pokud pronikneme intervaly
Jak už jsme výše naznačili, tento princip je jen dalším vyjádřením úplnosti reálných čísel. Ve světe racionálních čísel tento princip už neplatí, je snadné vytvořit vnořený soubor uzavřených intervalů racionálních čísel, který má prázdný průnik. Ještě se zde k těmto úvahám dvakrát vrátíme.
Příklad: Uvažujme množinu
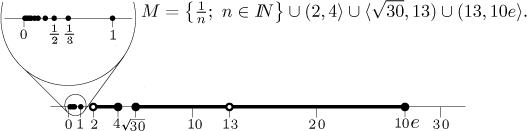
Bod
Bod
Teď uvažujme bod
Zkusme se podívat na jinou otázku. Když vezmeme nějaký bod a, jak
blízko k němu se množina M dokáže dostat? Například body 5 a 13 leží
oba mimo M, ale liší se v jedné věci. Množina M se dostane
libovolně blízko k 13 (jinak řešeno, můžeme "doskákat k 13" pomocí bodů z
M), ale u bodu 5 to neplatí, nejblíže k pětce se s množinou M
dostaneme v bodě odmocnina z 30. Podobný rozdíl vidíme u bodů 4 a 1, které
jsou oba z M. Zatímco k bodu 4 lze doskákat libovolně blízko pomocí
ostatních bodů z M, zatímco bod 1 je od zbytku M vzdálen
(nejbližší bod z M je
Jak se taková vlastnost dá vyjádřit pomocí okolí? Chceme, aby definice fungovala pro body z množiny i mimo ni, jinými slovy, když se zeptáme, "jak blízko je množina k danému bodu", tak nechceme, aby se nám do toho ten bod samotný pletl. To se snadno zařídí tím, že použijeme prstencová okolí. Bod je izolovaný, pokud existuje nějaké prstencové okolí, které je disjunktní s množinou M. Rozmyslete si, že to dobře ladí s těmi příklady výše, definice platí pro body 1 a 5 a není splněna pro body 4 a 13.
To, že se množina v nějakém bodě hromadí, pak lze vyjádřit takto: Každé
prstencové okolí tohoto bodu (jakkoliv malé) má neprázdný průnik s M.
Tohle zase platí pro body 4 a 13 a neplatí pro body 1 a 5. Všimněte si, že
je to splněno také pro
Už jsme předtím zmínili hranici této množiny, měli jsme pocit, že 1 a 4 jsou
na této hranici (a intuitivně vzato by na ní měla být i 2). Jak vyjádříme
matematicky pocit, že bod je na hranici množiny? To už není tak jasné. Jeden
možný požadavek by byl, že množina existuje na jedné straně a neexistuje na
druhé, ale ačkoliv toto není "špatně", tato definice by nebyla užitečná,
protože takto definovaná hranice by dobře neladila s jinými pojmy. Matematici
tedy dávají přednost jiné definici, a to takové, podle které by i 0 byla na
hranici, protože tam množina v jistém smyslu končí; také izolované body jako
1 by měly být hranice. Nápad vypadá takto: M by se měla dostat
libovolně blízko k takovému bodu (tentokráte může pomoci i samotný bod), ale
také vnějšek M by se měl dostat libovolně blízko k takovému bodu (a
zase si bod může pomoci sám, čímž se zajistí, že
Proč tak dlouhý příklad? Za prvé, doufáme, že jsme tím ukázali, jak se používají okolí. Pokud chceme mít možnost se trochu hýbat, aniž bychom vyskočili z "pěkného" místa, tak řekneme, že "existuje okolí, kde je pěkně". Pokud chceme říct, že nedokážeme bod od něčeho separovat, tak řekneme, že "se pro každé okolí něco stane". Toto jsou dvě nejtypičtější použití okolí a vidí se toho při práci s funkcemi spousta (tedy přinejmenším při teoretické práci). Druhý důvod je, že jsme neformálně uvedli užitečné pojmy a následující definice by měly dávat smysl.
Definice.
Uvažujme podmnožinu reálných čísel M a bod a.
Řekneme, že a je vnitřní bod M, jestliže existuje okolí U bodu a takové, že U je podmnožinou M.
Řekneme, že a je izolovaný bod M, jestliže existuje prstencové okolí P bodu a, které je disjunktní s M.
Řekneme, že a je hromadný bod či bod akumulace M, jestliže pro každé prstencové okolí P bodu a je průnik P s M neprázdný.
Řekneme, že a je hraniční bod M, jestliže pro každé okolí U bodu a je průnik U s M neprázdný a průnik U s M c neprázdný.Uvažujme podmnožinu reálných čísel M.
Definujeme vnitřek M, značeno M o nebo Int(M ), jako množinu všech vnitřních bodů M.
Definujeme uzávěr M, značeno, jako sjednocení M s množinou všech jejích hromadných bodů.
Definujeme hranici M, značeno ∂M, jako množinu všech hraničních bodů M.Řekneme, že množina M je otevřená, jestliže je rovna svému vnitřku (tj. jestliže je každý její bod vnitřní).
Řekneme, že množina M je uzavřená, jestliže je rovna svému uzávěru (tj. jestliže jsou všechny její hromadné body také jejími prvky).
Intuitivně, uzavřená množina je taková, že když začneme skákat pomocí jejích bodů, tak se nikdy nedostaneme někam mimo ni. Abychom si tyto pojmy vyjasnili, vrátíme se k příkladu.
Vnitřní body jsou body všech tří intervalů, které nejsou na jejich koncích, takže vnitřek množiny je
Izolované body jsou ty, které jsou typu
Když tyto hromadné body přidáme k M, dostaneme uzávěr
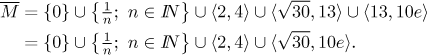
Protože se M nerovná svému vnitřku ani svému uzávěru, není tato množina otevřená ani uzavřená. Hranice M je
![]()
Všimněte si, že když přidáme ke vnitřku hranici, dostaneme uzávěr. To je obecný fakt, v obecnějších situacích definujeme hranici jako
![]()
Všimněte si také, že otevřený interval je otevřená množina, což je vlastně
důvod, proč se to tak jmenuje. Uzavřený interval je uzavřená množina,
všimněte si také, že vnitřkem intervalu (libovolného druhu) je otevřený
interval se stejnými krajními body, zatímco uzávěr libovolného intervalu je
uzavřený interval se stejnými krajními body. Poznamenejme, že interval
Dá se ukázat, že vnitřek libovolné množiny je otevřená množina (pokud je neprázdný), zatímco uzávěr libovolné množiny je uzavřený. Otevřené a uzavřené množiny hrají důležitou roli při práci s funkcemi.
Teď se ještě krátce vrátíme k pojmu hromadného bodu. V definici požadujeme, aby každé prstencové okolí obsahovalo nějaký bod z M, ale jakmile toto máme, tak se dá ukázat, že ve skutečnosti každé okolí hromadného bodu obsahuje dokonce nekonečně mnoho bodů z M. Z toho hned vyplyne, že konečné množiny nemohou mít hromadné body. Což takhle nekonečné množiny? Všimněte si, že množina celých čísel nemá hromadné body, takže ani tady situace není úplně jasná. Dá se nicméně ukázat, že konečnost množiny nebo to, že "uteče", jsou jediné možnosti, jak se vyhnout koncentraci bodů v nějakém místě.
Věta (Bolzano-Weierstrassova věta).
Každá omezená a nekonečná podmnožina reálných čísel má nějaký hromadný bod.
Je zajímavé, že se tato věta dá snadno dokázat pomocí Principu vložených intervalů, a naopak tuto větu můžeme použít k důkazu onoho Principu. Jinými slovy, jde o ekvivalentní vyjádření faktu, že reálná čísla tvoří úplnou množinu. To mimo jiné znamená, že se nemůžeme spoléhat na existenci hromadných bodů ve světe racionálních čísel. Tato věta má i další verze (například tu o konvergentní podposlounosti, viz sekce Základní vlastnosti v části Posloupnosti - Teorie - Limita), rovněž několik důležitých vět závisí na této vlastnosti, například Věta o extrémní hodnotě v sekci Spojitost v části Teorie - Reálné funkce.
Ještě jeden příklad použití topologie.
Definice.
Nechť M je podmnožina reálných čísel. Řekneme, že M je hustá v ℝ, jestliže pro každé reálné číslo a a každé prstencové okolí P bodu a je průnik P a M neprázdný.
Tahle definice je trochu dřevorubecká, dá se to říci mnohem elegantněji takto: Množina je hustá, jestliže je její uzávěr ℝ. Naše definice je trochu popisnější, intuitivně vzato je množina hustá, jestliže dokážeme všechna reálná čísla aproximovat s libovolnou přesností prvky oné množiny.
Racionální čísla jsou hustá v ℝ je tvrzení, které by mělo být jasné. Zajímavější je, že i docela malé části množiny racionálních čísel jsou pořád husté. Uvažujme například množinu
Tato množina je o dost menší, omezili jsme se pouze na zlomky, jejichž jmenovatele jsou ve tvaru 2n, ale stejně je to pořád množina hustá v ℝ. Podobná fakta mohou být docela užitečná v aplikacích, kdy chceme libovolně dobré aproximace, ale chceme na to malé množiny, například když chceme ukládat informace v počítači.
Docela pokročilá poznámka pro zvědavé, než přejdeme na další téma. Otevřené množiny jsme definovali přes vnitřek, což se zase definuje pomocí pojmu okolí. Ukazuje se, že se dá jít i opačným směrem. Pokud se rozhodneme, které množiny jsou otevřené, tak dostaneme stejná okolí; ne totožná coby množiny, ale stejná vzhledem k výsledkům, které pomoci nich můžeme dostat. A dostat toho můžeme dost. Pomocí okolí definujeme limity, a když na tom prostoru máme funkce, používáme okolí k definici derivace. Topologií prostoru míníme popis, které množiny jsou otevřené, či nějaký popis toho, co znamená být v okolí bodu. Obvyklý způsob, kterým se toto dělá, je definovat nějaký pojem vzdálenosti, pak vyjdou okolí tak, jak jsme je tady měli, ale můžeme také mít okolí bez vzdálenosti. Topologické prostory (prostory, kde máme otevřené množiny a okolí) mají limity a spoustu věcí, které tu děláme s funkcemi, je to velmi abstraktní teorie. Nicméně pokud rozumíte hlavním myšlenkám toho, co se tu dělalo, pak máte docela dobrou šanci alespoň zhruba vidět, co se děje obecně. Vysvětluje to také, proč se slovo topologie objevilo v názvu této sekce.
Když máme množinu s uspořádáním, můžeme se zeptat pár dobrých otázek o jejích podmnožinách.
Definice.
Uvažujme podmnožinu reálných čísel M. Nechť a je reálné číslo.
Řekneme, že a je dolní mez množiny M, jestližea ≤ m pro všechna m z M.
Řekneme, že a je horní mez množiny M, jestližea ≥ m pro všechna m z M.
Řekneme, že M je zdola omezená, jestliže má nějakou dolní mez.
Řekneme, že M je shora omezená, jestliže má nějakou horní mez.
Řekneme, že M je omezená, jestliže je omezená shora i zdola.
Uvažujme množinu M z příkladu výše. Je omezená shora, například
![]()
Na druhou stranu, množina přirozených čísel (coby podmnožina reálných) je omezená zdola (například nulou), ale ne shora, tudíž ani omezená. Je totiž jasné, že neexistuje reálné číslo x takové, aby pod ním ležela všechna přirozená čísla. Množina celých čísel není omezená v žádném smyslu.
Když máme množinu, hodí se někdy vědět, kde "začíná" a "končí".
Definice.
Uvažujme podmnožinu reálných čísel M. Nechť a je reálné číslo.
Řekneme, že a je nejmenší prvek M nebo že to je minimum M, značenoa = min(M ), jestliže je to dolní mez a náleží do M.
Řekneme, že a je největší prvek M nebo že to je maximum M, značenoa = max(M ), jestliže je to horní mez a náleží do M.
Jinými slovy, minimum je číslo, které leží v dané množině a všechna další
čísla této množiny jsou větší. Například minimum množiny přirozených čísel je
1, ale množina celých čísel minimum nemá. Podobně je 3 minimum množiny
Definice.
Uvažujme podmnožinu reálných čísel M.
Jestliže je M omezená shora, definujeme její supremum, značenosup(M ), jako nejmenší horní mez. Jestliže M není omezená shora, definujemesup(M ) = ∞.
Jestliže je M omezená zdola, definujeme její infimum, značenoinf(M ), jako největší dolní mez. Jestliže M není omezená zdola, definujemeinf(M ) = −∞.
Supremum a infimum jsou ty pravé pojmy k určení, kde množina začíná a končí.
Dá se ukázat, že pokud má množina maximum, pak je toto maximum také supremem
této množiny, podobně to funguje pro minimum a infimum. Pokud množina nemá
maximum, pak buď není omezená shora, v kterémžto případě se nějak táhne do
nekonečna a
Existuje způsob, jak si tyto pojmy představit. Nejprve se podíváme
na infimum. Jestliže množina není zdola omezená, tak se nějakým způsobem
táhne až doleva a
![]()
Hlavní výhoda suprema a infima je tato.
Věta.
Každá podmnožina reálných čísel má supremum a infimum a tyto jsou jednoznačně určeny.
Poznamenejme, že existenci suprema a infima lze odvodit z Principu vložených intervalů, naopak tento Princip vyplývá z existence suprema a infima. To je tedy další inkarnace faktu, že reálná čísla jsou úplná. Jinými slovy, ve světě racionálních čísel nemusíme mít supremum a infimum.
Supremum a infimum jsou v jistém smyslu limitní pojmy, což je pěkně vidět z
alternativní definice. Ta je sice méně elegantní, ale zato popisnější.
Uvažujme množinu M a číslo a. Toto číslo je supremum M,
jestliže
a) každý prvek x z M splňuje
b) pro libovolné okolí U bodu a je průnik U s M
neprázdný.
Analogicky se definuje infimum. Tato definice má výhodu v tom, že vlastně platí i pro případ nekonečného suprema/infima u neomezených množin. Když si připomeneme definice nerovnosti a okolí pro nekonečno (viz předchozí sekce), můžeme tu novou definici suprema aplikovat na a nekonečné a vidíme, že to funguje stejně jako původní definice. Za prvé, každé reálné číslo je menší než nekonečno, tudíž nekonečno vždy splňuje podmínku a). Pokud je také splněna podmínka b), pak není dotyčná množina shora omezená a podle první definice je nekonečno jejím supremem. Kdyby naopak podmínka b) pro nekonečno neplatila, pak je množina shora omezená a nějaké reálné číslo je jejím supremem.