Stejnoměrná spojitost

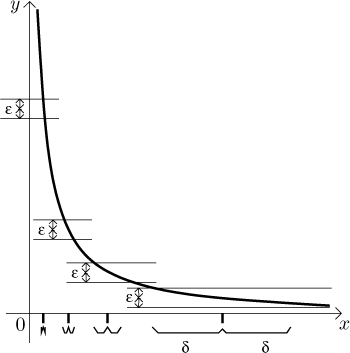
Když jsme definovali spojitost, byl to lokální pojem. Dokonce i definice spojitosti na množině se dělala tak, že se individuálně ověřila spojitost ve všech bodech. Existuje ale i čistě globální pojem, který zesiluje spojitost.

Definice.
Nechť f je funkce, nechť M je podmnožina jejío definičního oboru D( f ). Řekneme, že f je stejnoměrně spojitá na M, jestliže pro každé ε > 0 existuje δ > 0 takové, že pro všechna a,x z M splňující |x − a| < δ platí | f (x) − f (a)| < ε.

To je vlastně skoro totéž jako definice spojitosti, kterou jsme viděli předtím, je tu ale jeden kritický rozdíl. Pokud bychom chtěli obyčejnou spojitost na M, začali bychom tak, že bychom zvolili určitý bod a z M, a pak bychom ukázali, že umíme vyhrát všechny epsilon-delta hry. Hráli bychom tedy hry nezávisle pro každý bod zvlášť, což znamená, že pro totéž dané epsilon máme volnost vybírat různé delty pro rozličné body. U stejnoměrné spojitosti hrajeme hru simultánně pro všechny body z M. Je-li dána jedna konkrétní tolerance, musíme najít jedno delta tak, aby vyhrálo tuto epsilon-hru pro všechny body a z M.

Příklad: Uvažujme funkci f (x) = 1/x. Víme, že je spojitá na (0,∞). Není ale na tomto intervalu stejnoměrně spojitá. Na obrázku se snažíme ukázat, že když je nám dáno jedno konkrétní epsilon, pak jsme nuceni vybírat stále menší a menší delta, jak se s a blížíme k 0, a zdá se, že žádné delta nebude fungovat univerzálně.

Na druhou stranu, pokud se omezíme jen na interval ⟨1,∞), pak je tam již funkce stejnoměrně spojitá. Delta, které najdeme "na levém konci", bude fungovat všude.

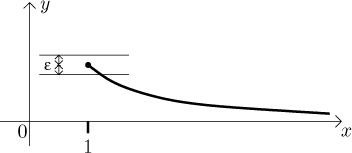
Můžeme se na to podívat ještě z jiné strany. Pokud budeme dělat kroky určité délky, pak v druhé situaci, ať už ten krok uděláme kdekoliv, funkce vždy roste či klesá o nějakou hodnotu, která nepřekročí jistou univerzální mez. Jinými slovy, když pro stejnoměrně spojitou funkci dostaneme délku kroku, můžeme udělat globální horní odhad toho, o kolik se funkce změní, ať už ten krok uděláme kdekoliv v dané množině. Na druhou stranu, v prvním obrázku vidíme, že když začneme dělat velmi malé kroky blíž a blíž k 0, pak funkce skáče víc a víc, bez nějaké meze pro velikost skoku.

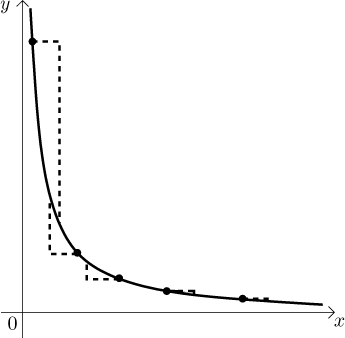
Bod a vlastně přestal být nějak speciální, pracujeme s páry bodů. Můžeme tedy přeformulovat definici takto. Funkce je stejnoměrně spojitá na dané množině, jestliže pro každou mez epsilon dokážeme najít delta takové, že libovolné dva body z množiny, které jsou dostatečně blízko (blíž než delta), po dosazení do funkce neudělají skok větší než ono epsilon.

Jak už jméno naznačuje, stejnoměrná spojitost je víc než spojitost.

Věta.
Funkce stejnoměrně spojitá na množině je tam nutně spojitá.

Příklad nahoře zase ukazuje, že ne každá spojitá funkce je stejnoměrně spojitá. Dokonce ani omezenost by nepomohla, funkce sin(1/x) je omezená a spojitá na omezeném intervalu (0,1), ale není tam stejnoměrně spojitá, protože má nekonečně mnoho vlnek o výšce 2 nahuštěných u nuly, což znamená, že i velice (libovolně) malým krokem lze dojít z vrcholu jedné vlny na spodek jiné (viz sin(1/x) v části Teorie - Elementární funkce).

Je několik způsobů, jak rozpoznat stejnoměrně spojité funkce bez nahánění delt.

Věta.
Funkce spojitá na omezeném uzavřeném intervalu je nutně stejnoměrně spojitá na této množině.

Všimněte si, že obě podmínky na množinu jsou třeba. Funkce 1/x není stejnoměrně spojitá ani na množině (0,1). Jako příklad neomezené uzavřené množiny můžeme vzít x² na ⟨0,∞), stejnoměrná spojitost selže podobně jako v příkladě nahoře, s tím rozdílem, že tam byl průšvih okolo 0, teď u x² se rychlost růstu zvyšuje okolo nekonečna.

Věta.
Jestliže je funkce spojitá na intervalu, derivovatelná na jeho vnitřku a tato derivace je tam omezená, pak je funkce stejnoměrně spojitá na tomto intervalu.

Všimněte si, že podmínka omezenosti derivace není nutná, protože existují stejnoměrně omezené funkce, jejichž derivace nejsou omezené na množině stejnoměrné omezenosti. Jedním příkladem je odmocnina z x na ⟨0,1⟩.

Se stejnoměrně spojitými funkcemi se lépe pracuje. Je to ale poněkud mimo záběr Math Tutoru, tak toho necháme.

Zpět na Teorie - Reálné funkce