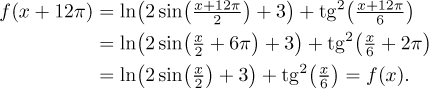Periodicita reálných funkcí: Přehled metod

Pro nalezení periodicity neexistuje algoritmus, obvykle si prostě tipneme a pak náš odhad buď potvrdíme nebo vyvrátíme. Máme zde tedy dvě témata. Za prvé, jak potvrdit či vyvrátit nějaký odhad, a za druhé, jak uhádnout periodu.

Potvrzení periodicity. Předpokládejme, že máme funkci f a máme rovněž podezření, že jisté T > 0 je perioda. Tento předpoklad se nejlépe ověří podle definice, takže musíme ukázat, že pro libovolné x platí f (x + T ) = f (x). Pokud se to povede, byl náš odhad správný. Pokud tato rovnost selže třeba i pro jediné x, pak toto T není perioda.

Teď dokážeme, že tangens je ve skutečnosti π-periodický pomocí pár goniometrických identit.

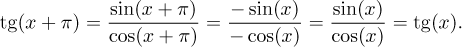
Odhad periody. Toto je založeno na dvou věcech. Tou první je znalost, že některé funkce jsou periodické s jistými základními periodami. Většina lidí zná vlastně jen čtyři takové funkce, jmenovitě sinus a kosinus se základní periodou 2π a tangens a kotangens se základní periodou π.

Druhou věcí je znalost toho, co se stane určité periodě, když začneme kombinovat funkce dohromady. Hodí se tato fakta:

 • Je-li f T-periodická, pak f (Ax + B) je (T/|A|)-periodická (všimněte si, že hodnota B je irelevantní, tj. posun v argumentu neovlivní periodicitu). Na druhou stranu Af (x) + B je zase T-periodická, takže transformace hodnot f nemá na periodicitu vliv.
 • Je-li f T-periodická, pak | f | je také T-periodická. Základní perioda se ale může změnit, například sin(x) je 2π-periodický, zatímco |sin(x)| je π-periodický.
Na druhou stranu f (|x|) nemusí být vůbec periodická, například tg(|x|) není periodický.
 • Je-li g T-periodická, pak složená funkce f (g) je T-periodická pro libovolnou funkci f. Zase poznamenejme, že se základní perioda může změnit, konec konců |sin(x)| je kompozice 2π-periodického sinu a neperiodického |x|. Na druhou stranu nám to, že je vnější funkce f periodická, neřekne nic o periodicitě složené funkce.
 • Je-li f T-periodická a g S-periodická, pak funkce f + g, f − g, f⋅g a f /g jsou R-periodické, kde R je nejmenší společný násobek S a T. Zase se může změnit základní perioda, například u tg = sin/cos se základní perioda zmenší na polovinu. Mimochodem, nejmenší společný násobek se dělá pro celá čísla, což T a S nemusí být, takže abychom byli přesní: R je nejmenší kladné číslo takové, že R/T a R/S jsou celá čísla.

Příklad: Určete periodicitu

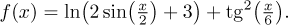
Řešení: Máme součet dvou funkcí, takže je začneme zkoumat individuálně.

Uvnitř prvního členu máme sinus s násobeným argumentem, takže podle jednoho z pravidel výše má sin(x/2) periodu 2⋅2π = 4π. Tato funkce je pak zvětšena dvakrát a posunuta nahoru o 3, což periodu neovlivní. Nakonec na to aplikujeme logaritmus jako vnější funkci v kompozici, takže výsledek je zase 4π-periodický. Mimochodem, pořád je to základní perioda, logaritmus to nezmění, ale to teď není podstatné.

V druhém členu máme vevnitř tangens s násobeným argumentem, takže původní perioda π se vynásobí 6 podle pravidla výše. Proto je tg(x/6) 6π-periodický. Tato funkce je pak umocněna na druhou, což už periodu neovlivní.

Sčítáme tedy dva členy, jeden je 4π-periodický, druhý je 6π-periodický. Pravidlo říká, že součet by měl mít jako peridou nejmenší společný násobek, takže odhadneme, že daná funkce je 12π-periodická.

Teď ověříme, že je tento odhad správný:

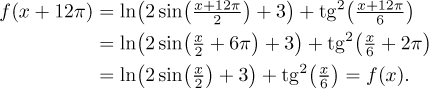
Důkaz je hotov, náš odhad byl správný. Je to mimochodem také základní epizoda, ale to se obecně nedokazuje nijak snadno, takže toho necháme.

Pro další příklady odkazujeme na Řešené příklady.

Spojitost
Zpět na Přehled metod - Základní vlastnosti reálných funkcí