Spojitost reálných funkcí: Přehled metod

Jsou dva způsoby, jak zkoumat spojitost - globální a lokální.

Globální spojitost.

O mnoha funkcích víme, že jsou spojité na svých definičních oborech, jmenovitě všechny elementární funkce. Víme také, že když elementární funkce kombinujeme operacemi, spojitost se zachovává. Můžeme tak určit spojitost libovolné funkce, která je tvořena elementárními funkcemi.

Příklad: Funkce

je spojitá na svém definičním oboru D( f )=(−∞,5) ∪ (5,∞), protože je na něm vytvořena kombinováním elementárních funkcí.

Poznamenejme, že pro spojitost potřebujeme oboustranná okolí, takže ona procedura popsaná výše funguje jen na otevřených množinách. Pokud definiční obor obsahuje nějaké krajní body, dostaneme tam pouze jednostrannou spojitost. To může mít dalekosáhlé důsledky v komplikovanějších situacích (třeba funkce definované rozpisem), takže je bezpečnější používat globální přístup pouze u otevřených množin a dělat koncové body individuálně (viz lokální spojitost níže).

Funkce definované rozpisem. Tyto funkce jsou definováný různými vzorci na (typicky) disjunktních množinách. Jestliže jsou všechny vzorce spojité na množinách, kterých se týkají, pak je daná funkce definovaná rozpisem spojitá na sjednocení vnitřků těchto množin. Zde je důležité si připomenout, že když je funkce spojitá na intervalu (a,b⟩ a na intervalu (b,c), pak nemusí být spojitá na jejich sjednocení (a,c)! Důvod je jednoduchý: Spojitost na (a,b⟩ dává spojitost v b pouze zleva, z tohoto intervalu nedostaneme žádnou informaci o spojitosti v b zprava, a také nedostaneme informaci o spojitosti zprava v b z intervalu druhého, protože b vůbec nenáleží do (b,c). Tyto "spojovací body" musí být dělány lokálně, viz další téma.

Lokální spojitost.

Je dána funkce f a bod a z jejího definičního oboru a chceme vědět, jestli je f spojitá v a. Jsou dvě možnosti.

Případ 1. Existuje nějaké okolí U bodu a, na kterém je daná funkce definována nějakým výrazem, jehož spojitost je již známá. Pak je f také automaticky spojitá v a. Například funkce f z předchozího příkladu je spojitá v a = 13.

Případ 2. Neexistuje takové okolí. V nejtypičtějším případě to znamená, že je funkce definovaná rozdílně napravo a nalevo od bodu a. Například absolutní hodnota |x| uvažovaná v a = 0 má tuto vlastnost, protože je definována jako x napravo a jako -x nalevo od 0.

V takovém případě určujeme spojitost a případně klasifikujeme objevivší se nespojitost takto:

Krok 1. Určíme obě jednostranné limity v a a číslo f (a).

Krok 2. Porovnáme ta tři čísla z Kroku 1 a dostaneme odpověď. Jsou čtyři možnosti:
 • Obě jednostranné limity konvergují, jsou stejné (takže také dávají (oboustrannou) limitu) a jsou rovněž rovny f (a). Pak je funkce spojitá v a.
 • Obě jednostranné limity konvergují, jsou stejné (takže také dávají (oboustrannou) limitu), ale nerovnají se f (a). Pak funkce není spojitá v a, má tam odstranitelnou spojitost.
 • Obě jednostranné limity konvergují, ale nerovnají se. Pak (oboustranná) limita neexistuje, funkce není spojitá v a, má tam skokovou nespojitost.
 • Alespoň jedna z jednostranných limit nekonverguje. Pak funkce není spojitá v a, má tam podstatnou nespojitost.

Jednostranná spojitost

Abychom rozhodli, zda je daná funkce spojitá v bodě a zleva, nejprve spočítáme limitu v a zleva a f (a), potom je porovnáme.

Pokud limita zleva konverguje a rovná se f (a), pak je funkce spojitá v a zleva. Jinak funkce není spojitá v a zleva. Pro jednostrannou spojitost neklasifikujeme nespojitosti.

Spojitost zprava se dělá obdobně.

Příklad: Určete spojitost funkce

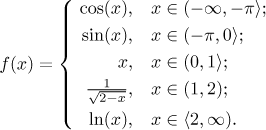
Řešení: Začneme tím snadným, globální spojitostí. Pro každý interval uvedený v definici je funkce f definovaná určitou funkcí na tomto intervalu, takže je tam také spojitá. Protože musíme být opatrní a pracovat s otevřenými množinami, dostáváme závěr, že je funkce spojitá na množině

(−∞,−π) ∪ (−π,0) ∪ (0,1) ∪ (1,2) ∪ (2,∞).

Jak je to s body, které v této množině chybí? Musíme použít lokální přístup a prozkoumat spojitost v bodech -π, 0, 1 a 2. Najdeme tedy jednostranné limity a funkční hodnoty v těchto bodech. Připomeňme, že při výpočtu jednostranných limit musíme vždy použít správné vzorce.

Závěr:
 • V a = −π je skoková nespojitost, ale f je tam spojitá zleva.
 • V a = 0 je f spojitá.
 • V a = 1 je f spojitá.
 • V a = 2 je podstatná nespojitost, ale f je tam spojitá zprava.

Když to tedy dáme dohromady s globálním krokem, dostaneme

Odpověď: f je spojitá na množině

(−∞,−π) ∪ (−π,2) ∪ (2,∞).

Je také spojitá zleva v -π a spojitá zprava v 2.

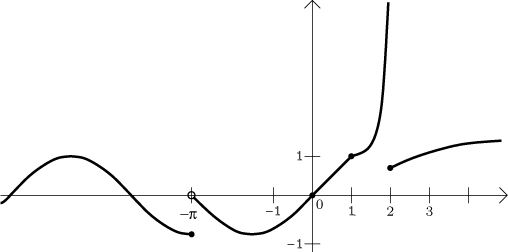
Obrázek ukáže, co se vlastně děje, ale všimněte si, že jsme ho vůbec nepotřebovali k nalezení výsledku.

Pro další příklady odkazujeme na Řešené příklady.

Prostota a inverzní funkce
Zpět na Přehled metod - Základní vlastnosti reálných funkcí