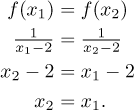
Zkoumání prostoty, nalezení inverzní funkce u reálných funkcí: Přehled metod

Jsou dvě hlavní metody pro určení, zda je funkce f prostá.

Podle definice. Začne se rovnicí f (x1) = f (x2). Má jedno triviální řešení x1 = x2, finta je v tom, že musíme zjistit, zda také neexistuje nějaké další řešení, kdy jsou x1 a x2 rozdílné. Pokud ano, pak funkce není prostá. Pokud je triviální řešení tím jediným, pak je funkce prostá.

Pomocí teorie. Máme několik vět, které zaručí, že je daná funkce prostá. Asi nejsnadnější a zároveň velmi užitečná je tato:

Jestliže je funkce na nějaké množině ryze monotonní, pak tam musí být prostá.

To mimo jiné znamená, že jestliže je funkce spojitá na nějakém intervalu I, diferencovatelná na jeho vnitřku, ta derivace není nikde nula a má všude stejné znaménko, pak je tato funkce prostá na I.

Inverzní funkce

Jakmile máme funkci, která je někde prostá, můžeme najít její inverzní funkci vyřešením rovnice y = f (x) pro x, dostaneme x = f−1( y).

Příklad: Rozhodněte, zda je funkce f (x) = 1/(x − 2) prostá, a pokud ano, najděte její inverzní funkci.

Řešení: Nejprve ukážeme, že je funkce prostá. Protože vypadá dost jednoduše, zkusíme to podle definice.

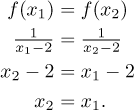
Protože všechny kroky byly ekvivalentní, existuje jen to jedno řešení a funkce je prostá.

Všimněte si, že kdybychom to chtěli zkusit přes teorii, měli bychom problém, protože definiční obor funkce je D( f ) = (−∞,2) ∪ (2,∞). Na každém intervalu je derivace −1/(x − 2)2 záporná, takže je tam funkce klesající a tedy i prostá. Bohužel, když máme funkci prostou na dvou intervalech, nemůžeme nic říct o prostotě f na jejich sjednocení, protože na nich může klidně nabývat stejných hodnot. To se tedy v tomto případě neděje, ale vidíme, že přístup přes monotonii pracuje dobře jen na jednotlivých intervalech, na komplikovanějších množinách musíme buď použít definici, nebo udělat víc práce, například sestrojit graf.

Každopádně teď máme funkci prostou na svém definičním oboru a chceme najít její inverzní funkci:

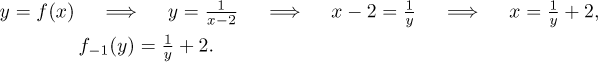
Kdybychom teď chtěli pracovat jen s tou inverzí bez vztahu k původní funkci f, nemuseli bychom si původ inverze připomínat proměnnou y, mohlo by se víc hodit přejmenovat proměnnou na x:

Důležité vlastnosti:
1. Definiční obor a obor hodnot se prohodí:

D( f−1) = R( f ),     R( f−1) = D( f )

2. Graf inverzní funkce se dostane tak, že se vezme graf f a překlopí okolo hlavní diagonály y = x. Pokud se to udělá správně, pak musí monotonie f a její inverze souhlasit. Přesně, pokud je nějaká část grafu (na intervalu) rostoucí, pak po překlopení musí být tato část zase rostoucí; totéž funguje pro klesající.

Příklad: Nalevo je graf nějaké prosté funkce f, napravo její inverze.

 

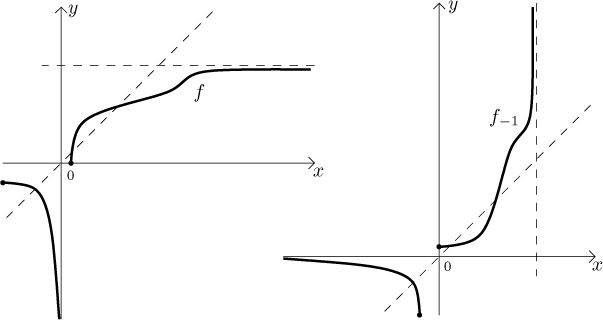
Pro další příklady odkazujeme na Řešené příklady.

Transformace a odhad grafu.
Zpět na Přehled metod - Základní vlastnosti reálných funkcí