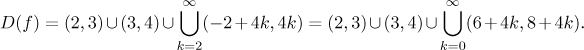Příklad: Určete definiční obor následující funkce:

Řešení: Máme obecnou mocninu (tu odmocninu), takže musíme začít tím, že si ji přepíšeme pomocí triku "e na ln":

Teď jsme připraveni hledat problémy:

1. Vnější logaritmus vyžaduje, aby byl jeho argument kladný: log₃(log₂(x)) > 0.

2. Prostřední logaritmus také žere pouze kladné argumenty: log₂(x) > 0.

3. Vnitřní logaritmus také chce, aby byl argument kladný: x > 0.

4. Přejdeme k exponenciále, její argument může být libovolný, takže se podíváme na argument samotný. Nejprve vidíme malý zlomek, jeho jmenovatel nesmí být nulový: x² ≠ 0, neboli x ≠ 0.

5. Pak máme logaritmus, jeho argument by měl být kladný:

6. Kosinus sežere cokoliv, jdeme dál. Další člen je 2^x, který přijme libovolné číslo. Přejdeme tedy k poslednímu členu, je to zlomek, potřebujeme tedy nenulový jmenovatel.

7. Logaritmus vyžaduje

neboli x > 1.

Teď se podíváme blíže na podmínky, které vyžadují další práci.

Podmínka 1: Pokud povýšíme obě strany nerovnice jako argumenty 3^x a zkrátíme "3^log₃", dostaneme log₂(x) > 3⁰ = 1.

Teď zase obě strany povýšíme jako argumenty 2^x a dostaneme x > 2¹ = 2.

Podmínka 2: Pokud povýšíme obě strany nerovnosti jako argumenty 2^x a zkrátíme "2^log₂", dostaneme x > 2⁰ = 1.

Všimněte si, že podmínky 1, 2 a 3 jsou podobného typu a postupně méně a méně restriktivní, takže nakonec během pronikání můžeme druhou a třetí podmínku ignorovat a pracovat pouze s první, x > 2.

Podmínka 5: Toto se nejlépe dělá tak, že uvažujeme cos(y) a zeptáme se, kdy je kladný. Pohledem na graf kosinu zjistíme, že y musí náležet do nebo nějakého posunu tohoto intervalu o 2π. Vyjádřeno jazykem nerovností:

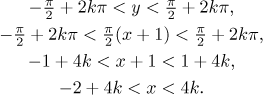
Proto musí x ležet v intervalu (−2,0) něbo nějakém posunu o 4, neboli

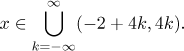
Podmínka 6: Povýšením obou stran na exponenciálu a zkrácením "e^ln" dostaneme podmínku (x − 1)/2 ≠ e⁰ = 1, tedy x ≠ 3.

Teď pronikneme všechny podmínky

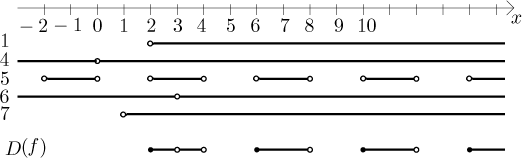
a dostaneme odpověď:

Další příklad
Zpět na Řešené příklady - Reálné funkce