Příklad: Pro následující funkci určete, zda je prostá, a pokud ano, najděte příslušnou inverzní funkci. Prozkoumejte také její monotonii.

Řešení: Nejprve si všimněme, že definiční obor f jsou všechna reálná čísla kromě −1.

K určení prostoty použijeme standardní postup. Vezmeme x₁, x₂ z definičního oboru, budeme předpokládat, že po dosazení do f dají stejnou hodnotu, a uvidíme, jestli existuje i jiné řešení než to triviální.

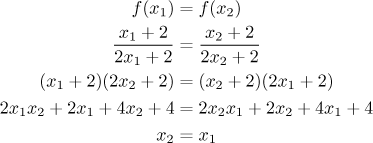
Vidíme, že jediný způsob, jak dostat stejnou hodnotu, je začít ze stejného místo, což ukazuje, že funkce je prostá.

Teď najdeme inverzní funkci řešením rovnice y = f (x) pro x:

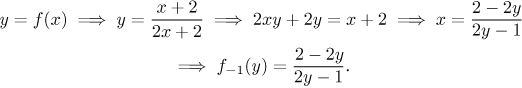
Teď potřebujeme prozkoumat monotonii. Zatím známe jen definici, takže zkusíme dokázat jednu ze dvou příslušných implikací. Vezmeme libovolná dvě čísla x₁ < x₂ z definičního oboru a zkusíme dokázat, že f (x₁) < f (x₂), což by dokázalo, že f je rostoucí, nebo že vždy f (x₁) > f (x₂), což by ukázalo, že f je klesající; je také možné, že ani jedno z toho není možné, pak by asi byl s monotonií nějaký problém.

Jak dokážeme takové implikace? Začneme nerovností x₁ < x₂ a zkusíme použít ekvivalentní operace k vytvoření vzorce pro f na obou stranách. Bohužel, zde hned narážíme na problém, protože vzorec pro f obsahuje proměnnou x na dvou místech a nemáme ekvivalentní úprav, které by nějak zvýšily výskyt jedné proměnné v nerovnici.

Naštěstí je daná funkce podíl lineárních funkcí, na což máme náš oblíbený trik: Vydělíme se zbytkem. V tomto konkrétním případě dokonce máme alternativu k normálnímu algoritmu pro dělení polynomů, jmenovitě vyrobíme výraz ze jmenovatele také v čitateli, nejprve vytvoříme příslušný počet x pomocí dělení/násobení, pak použijeme přičtení/odečtení, abychom upravili absolutní člen. Vypíšeme všechny detaily, při troše zkušeností to ale jde dost rychle.

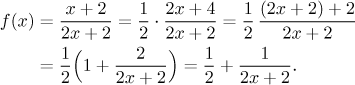
Tento typ výrazu už můžeme zkusit vyrobit, vždy začneme od x v tomto výrazu a pak jdeme ven podle pořadí výpočtu. Nejprve vynásobíme obě strany dvěma, pak přičteme 2.

Další krok je přesunout lineárky do jmenovatelů na opačných stranách nerovnice. To se dělá vydělením celé nerovnice příslušným členem, ale tady narážíme na problém. Když dělíme nerovnost, znaménko členu, kterým dělíme, rozhoduje, zda máme prohodit směr nerovnice nebo ne. Zde jej neznáme, takže se jako obvykle podíváme na všechny možnosti. Začneme předpokladem, že x₁ > −1, pak také x₂ > −1, protože je větší. S touto volbou jsou oba členy (2x + 2) v nerovnici kladné.

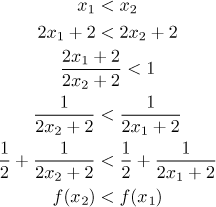
Vydělili jsme nejprve členem (2x₂ + 2), pak (2x₁ + 2), nakonec jsme přičetli k oběma stranám 1/2. Dokázali jsme tak jednu z implikací, o které jsme měli zájem, ale povedlo se to pouze za předpokladu, že jsou obě proměnné > −1. Naštěstí pro nás se toto dá přepsat ve formě, že obě proměnné náleží do určité množiny, jmenovitě do intervalu (−1,∞). Ukázali jsme tedy, že pro všechny páry x₁ < x₂ z (−1,∞) se po aplikování funkce prohodí pořadí (větší argument dává menší hodnotu), neboli jsme právě dokázali, že f je klesající na intervalu (−1,∞).

Teď se musíme podívat na druhou alternativu, když x₁ < −1. Když vydělíme odpovídajícím členem, musíme změnit směr nerovnosti, protože ten člen je záporný.

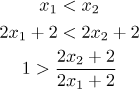
V dalším kroku bychom rádi vydělili členem (2x₂ + 2), ale na rozdíl od prvního případu zde nemáme relevantní informaci o x₂, protože tentokráte to neplyne z x₁ < −1.

"Dobrý" případ je, když také x₂ < −1. Za tohoto předpokladu dokončíme výpočet, zase musíme při dělení změnit směr.

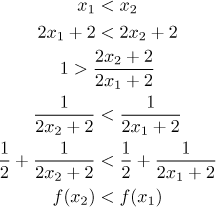
Stejně jako předtím se změnil směr srovnání a podmínka "x₁ < −1 a x₂ < −1" je intervalového typu, takže jsme vlastně zase dokázali, že f je klesající na intervalu (−∞,−1).

Závěr tedy zatím je, že f je klesající na (−∞,−1) a na (−1,∞). Pokud by otázka zněla "identifikujte intervaly monotonie", tak už bychom byli hotovi, protože v tomto směru nelze udělat víc: Tyto dvě množiny dávají definiční obor a nelze je spojit do jednoho intervalu. Pro většinu aplikací by tato analýza byla dostatečná.

Máme ale vyšetřovat, takže možná se po nás chce víc. Můžeme ty dvě množiny spojit do jedné (pak už to nebude interval) a prohlásit, že funkce je klesající, popř. nerostoucí na definičním oboru? (Vzhledem k monotonii na jednotlivých podintervalech nic jiného nepřichází v úvahu.) To teď neumíme rozhodnout, je třeba mít nějaké další informace.

Což nás přivádí k poslednímu případu pro proměnné, když x₁ < −1 a x₂ > −1.

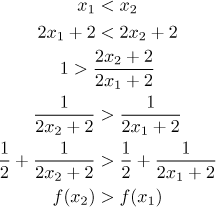
Tentokráte dostáváme implikaci, která naznačuje růst, což nevypadá dobře. Tvrdíme, že daná funcke není monotonní na svém definitčním oboru. Nemůže být rostoucí či neklesající kvůli svému chování na oněch dvou intervalech. Možnost, že je klesající či nerostoucí zase vylučuje ten poslední výpočet. Pokud například zvolíme x₁ = −2 a x₂ = −2, pak x₁ < x₂, ale snadno se přesvědčíme, že f (x₁) > f (x₂).

Poznamenejme, že ryzí monotonie implikuje prostotu, z těch klesajících částí tedy dostaneme, že f je prostá na (−∞,−1) a také na (−1,∞), ale víme, že intervaly prostoty nejdou spojovat ve větší množiny bez dalšího zkoumání.

Poznamenejme také, že "vydělený" tvar podílu lineárních funkcí usnadňuje i další výpočty. Zkusme se krátce vrátit k prvním dvěma tématům. Nejprve ověříme, že je funkce prostá:

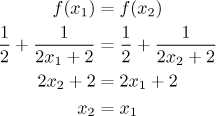
Teď najdeme inverzní funkci.

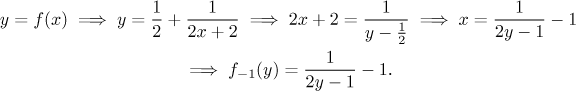
Snadno se nahlédne, že jsme dostali stejnou funkci jako předtím.

Další příklad
Zpět na Řešené příklady - Reálné funkce