Příklad: Pro následující funkci určete, zda je prostá, a pokud ano, najděte příslušnou inverzní funkci. Prozkoumejte také její monotonii.

Řešení: Definičním oborem této funkce je celá reálná osa. Pro ověření prostoty vezmeme rovnici f (x₁) = f (x₂) a podíváme se, jestli jsou jiná než triviální řešení.

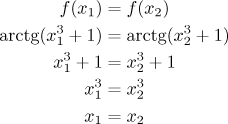
V druhém kroku jsme použili toho, že arctg je prostá funkce, takže jestliže se rovnají hodnoty, musí se rovnat i argumenty. Stejný argument se použil v posledním kroku, tentokráte se použila prostota třetí mocniny. Vidíme, že jediné řešení je to triviální, funkce je proto prostá.

Teď najdeme inverzní funkci vyřešením rovnice y = f (x) pro x.

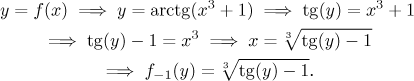
Poznámka: Když jsme hledali inverzní funkci, měli jsme v jednu chvíli rovnost y = arctg(z) a změnili jsme ji v z = tg( y).

Všimněte si, že toto funguje jen pro arkustangens. Pokud bychom měli y = tg(z), pak není možné usoudit, že z = arctg( y)! Důvod je, že k nalezení inverzní funkce k tangensu jsme museli omezit definiční obor tangensu na . Tangens a arkustangens jsou navzájem inverzní pouze za předpokladu, že je proměnná tangensu z tohoto intervalu. V rovnici y = arctg(z) automaticky platí, že y je z tohoto intervalu, protože je to hodnota arkustangensu. Na druhou stranu, je-li dána rovnice y = tg(z), není nijak zaručeno, že z je z tohoto intervalu a vlastnost inverze mezi tangensem a arkustangensem se tedy nedá aplikovat.

Abychom prozkoumali monotonii podle definice, začneme s párem x₁ < x₂ z definičního oboru a podíváme se, jestli nedokážeme dostat nějakou nerovnost mezi funkčními hodnotami. To uděláme tak, že se pokusíme upravovat nerovnost a vytvořit danou funkci na obou stranách pomocí elementárních operací.

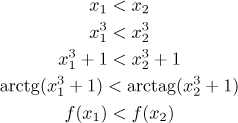
Všimněte si, že jsme v druhém kroku aplikovali třetí mocninu na obě strany, což je povolená operace, protože x³ je rostoucí funkce, tj. dělá z menších argumentů menší hodnoty. Ze stejného důvodu jsme pak mohli aplikovat rostoucí arkustangens v posledním kroku.

Každopádně jsme ukázali, že pro libovolná dvě čísla z definičního oboru daná funkce při aplikaci zachovává jejich pořadí (menší na menší, větší na větší), takže jsme dokázali, že je tato funkce rostoucí na celé reálné ose.

Poznámka: Pro důkaz monotonie se také můžeme podívat na znaménko derivace:

Je vždy kladná a z toho již plyne, že je funkce rostoucí, viz Derivace - Teorie - Věta o střední hodnotě a spol..

Poznamenejme, že jakmile máme striktní monotonii na definičním oboru, již z toho vyplyne protota funkce.

Další příklad
Zpět na Řešené příklady - Reálné funkce