Příklad: Pro následující funkci určete, zda je prostá, a pokud ano, najděte příslušnou inverzní funkci. Prozkoumejte také její monotonii.

Řešení: Definiční obor této funkce je celá reálná osa. Prostotu funkce rozhodneme tak, že vezmeme rovnici f (x₁) = f (x₂) a zjistíme, zda existuje i jiné řešení než triviální.

No a to je konec, nemáme sebemenší nápad, co s tímhle algebraicky provést.

Naše jediná šance je nějaká pomoc od teorie. Můžeme říct něco o monotonii? Tohle je vlastně další část otázky, takže to rovnou uděláme. Abychom určili monotonii podle definice, začneme s párem x₁ < x₂ z definičního oboru a aplikováním operací na tuto nerovnost zkusíme vytvořit danou funkci na obou stranách. Zde to nevypadá tak snadně, jako v předchozích příkladech, protože se proměnná vyskytuje ve funkci na třech místeh a operace s nerovnostmi nedoolují přidat více x.Naštěstí pro nás zde máme sčítání členů a nerovnosti lze sečíst za předpokladu, že ukazují stejným směrem.

Začneme tedy se základní nerovností x₁ < x₂ a aplikujeme na ni třetí mocninu, což můžeme (a beze změny směru nerovnice), protože je to rostoucí funkce. Jinými slovy, mění menší čísla na menší třetí mocniny, větší čísla na větší třetí mocniny, takže nerovnost přežije. Podobně můžeme aplikovat i pátou mocninu na původní rovnici a pak je všechny sečíst:

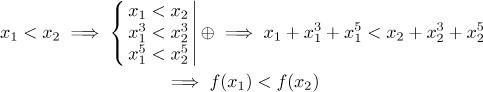
Právě jsme dokázali, že pro libovolná dvě čísla z definičního oboru daná funkce zachovává jejich pořadí, proto je tato funkce rostoucí na definičním oboru.

Poznámka: Zde je asi snažší použít naši oblíbenou metodu pro určování monotonie a podívat se na derivaci:

Protože je derivace na intervalu ℝ kladná, je funkce na této množině rostoucí (viz Derivace - Teorie - Věta o střední hodnotě a spol.).

Zpět k původní otázce. Protože je funkce striktně monotonní na svém definičním oboru, je také prostá.

Abychom našli inverzní funkci, řešíme rovnici y = f (x) pro x.

A je konec, nemáme absolutně žádný nápad, co s tím dělat. Víme, že inverzní funkce existuje, ale neumíme ji najít.

Další příklad
Zpět na Řešené příklady - Reálné funkce