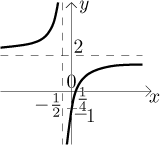
Příklad: Pomocí transformací odhadněte graf následující funkce:

Řešení: Nejprve musíme identifikovat základní funkci, s jejímž tvarem začneme. To ale tady není možné, protože se proměnná x vyskytuje dvakrát. Proces odhadování vždy začne s nějakou elementární funkcí, ve které je proměnná jen jednou, a transformace pak neumožní její výskyt rozmnožit.

Naštěstí pro nás se z toho v tomto případě můžeme vyvléknout. Máme podíl lineárních funkcí a takový výraz je obvykle mnohem příjemnější, když vydělíme se zbytkem, zde ale použijeme náš oblíběný trik a vyrobíme si jmenovatel v čitateli. nejprve vyrobíme správný počet x dělením/násobením, pak upravíme absolutní člen přičtením/odečtením.

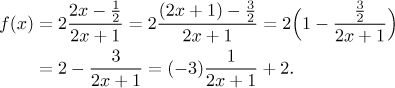
Ten poslední krok jsme udělali, abychom výraz připravili pro analýzu. Máme teď jen jedno x a jsme připraveni identifikovat základní funkci. Víme, že výraz ve jmenovateli lze vyrobit změnou měřítka a posunem, takže jej můžeme ignorovat a podívat se na (−3)⋅1/x + 2. Zase vidíme, že násobení (−3) a posun o 2 se dají ignorovat, tentokráte jsou aplikovány na funkci 1/x, což je naše základní funkce.

Začneme tedy grafem funkce 1/x a nejprve transformujeme její argument. Jsou tam dvě transformace, násobení číslem 2 a posun o 1. Jsou počítány právě v tomto pořadí a pravidlo pro argument říká "od posledního k prvnímu", takže bychom měli nejprve posunout o 1 doleva a pak změnit měřítko funkce, budeme ji dvakrát zmenšovat ve vodorovném směru (směrem k ose y). Ověříme, že toto pořadí opravdu vytvoří, co by mělo, pomocí nahrazovacího značení:

x → x + 1 → (2x) + 1.

V každém kroku jsme nahradili samotné x odpovídajícím transformačním výrazem a dostali jsme přesně to, co potřebujeme, takže pořadí je správné. Jdeme na to.

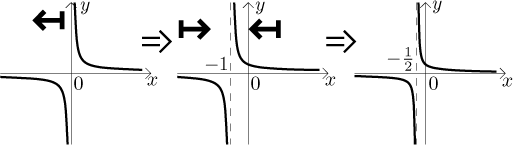
Rychle si ověříme, že jsme zatím neudělali nějakou zásadní botu: V definičním oboru je díra v bodě −1/2, což zdá se souhlasí s naším obrázkem.

Teď je načase aplikovat transformace na hodnotu. Jsou dvě, změna měřítka o (−3) a posun o 2, jsou počítány v tomto pořadí. Pravidlo pro hodnotu říká "od prvního k poslednímu", takže bychom měli aplikovat transformace v témže pořadí. Nejprve změna měřítka, natáhneme funkci ve svislém směru, od osy x, třikrát, a kvůli zápornému znaménku také překlopíme obrázek okolo osy x. Pak posuneme obrázek nahoru o 2.

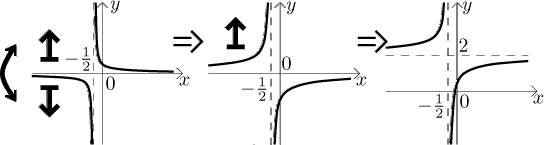
A to by mělo být ono. Doporučujeme ale, aby se udělaly ještě dvě věci.

Nejprve ověříme, že náš odhadnutý graf není zcela mimo tím, že spočítáme hlavní rysy. Jsou dva výrazné rysy, svislá a vodorovná asymptota. Svislá asymptota je v díře v definičním oboru −1/2, což nás obrázek zachytil dobře, a když spočítáme jednostranné limity v −1/2 (což zkušený student udělá z hlavy, aniž by něco psal), uvidíme, že směry, ve kterých tam graf utíká, jsou správně, jde do nekonečna nalevo a mínus nekonečna napravo od −1/2.

Pak se podíváme na limitu funkce v nekonečnu a mínus nekonečnu a dostaneme 2 (což je zase snadné, stačí se na výraz podívat), takže máme i vodorovnou asymptotu správně. Můžeme si teď být docela jisti, že jsme ten obrázek udělali dobře.

Toto odhadování grafu je v rukou zkušeného studenta dost spolehlivé, takže když už máme pěkný a správný graf, možná by stálo za to jej trochu upravit, abychom správně zachytili i další informaci. Jsou dva výrazné body, průniky s osami. Vypočítáme tedy průnik s osou y: f (0) = −1, a také průnik s osou x: f (x) = 0 dává x = 1/4. Upravíme pdole toho graf a přidáme popisky, teď máme velice dobře vypadající graf.

Další příklad
Zpět na Řešené příklady - Reálné funkce