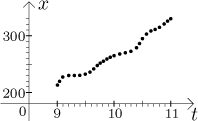
Představte si následující situaci. Někam jedeme a z nějakého důvodu se rozhodneme sledovat, kolik jsme ujeli. Asi nejjednodušší způsob je značit si čísla objevující se na tachometru. Předpokládejme například, že když vyjedeme, je tam číslo 213. To znamená, že jestliže chceme vědět, kolik jsme v určitý okamžik ujeli, tak prostě odečteme 213 od čísla, které se zrovna objevilo na palubní desce.
K doplnění situace ještě předpokládejme, že začneme v 9 hodin a do cíle
dojedeme v 11. Abychom to dělali správně, budeme čas převádět do desítkové
soustavy, například
Takže jedeme a zapisujeme si páry "čas - číslo na tachometru v daný čas", na konci pak máme tabulku s mnoha takovými páry. Čím častěji tak měříme, tím přesnější tato tabulka bude a tím víc informací o výletě budeme mít. Jeden dobrý způsob, jak si tato data zobrazit, je vynést je do grafu, použijeme osy t pro čas a x pro číslo na tachometru:

Mohli bychom samozřejmě použít nějaký přístroj, řekněme počítač, který by tato data automaticky zaznamenával, dostali bychom páry "čas - kilometry" s frekvencí tisícovek za sekundu. Ale i tak by byla výsledná tabulka a graf "diskrétní" a s "dírama", jinými slovy bychom měli data pro určité časy. Pokud ale chceme použít sílu matematiky na naši situaci, potřebovali bychom měření pro všechny možné časy mezi 9 a 11 (což je nekonečně mnoho a tedy reálně nemožné). Musíme teď proto zkusit udělat malou abstrakci a představit si, že taková věc je možná, že nějak dostaneme nekonečnou tabulku párů "čas - číslo" pokrývající všechny časy mezi 9 a 11. Můžeme si například představit, že stále zvyšujeme přesnost a rychlost měřícího přístroje a postupně "zaplňujeme díry" ve grafu.
Dostaneme tak graf s opravdu nepřerušovanou čárou.
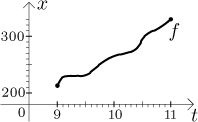
Tato abstraktní množina nekonečně mnoha měření je to, co nazýváme funkcí, je
to jakýsi předpis, který bere argument (v tomto případě čas) a dává
odpovídající číslo. Protože pro argumenty této funkce používáme čas, bereme je
z množiny reálných čísel. Výsledky jsou také reálné, máme tedy reálnou
funkci; nazveme ji f. Zápis
Dospěli jsme k pojmu funkce, teď si připomeneme nějaké s ní spojené pojmy.
Začneme s definičním oborem, množinou argumentů, pro které má funkce
smysl (tj. čísel t, která lze dosadit do funkce). Zde nemáme žádnou
informaci o tom, co se stalo před 9 a po 11 (musíme se také dohodnout, jak
budeme interpretovat čísla jako 150 a −3, ale to není problém, seřadíme dny
jeden za druhým a číslujeme čas postupně, takže například −3 je 21
předchozího dne, zatímco 25.6666... je
Jaké jsou hodnoty funkce funkce f ? Protože tachometr začal s 213 a skončil s 330, nemohly naše měření ukázat čísla větší než 330 a menší než 213 (pokud jsme tedy nešaškovali s tachometrem). Můžeme také tvrdit, že se všechna čísla mezi 213 a 330 musí v naší tabulce objevit, protože auto nemůže skočit z jedné pozice na druhou, aniž by prošel všemi místy mezi. Odhadneme proto, že obor hodnot funkce f je uzavřený interval mezi 213 a 330, což bychom zapsali takto (zase dáváme přednost prvnímu značení):
Je tato funkce prostá? V praxi se
často lépe zkoumá otázka, zda daná funkce neselže vlastnost prostoty, což se
dá formulovat následovně: Je možné, aby dva rozdílné argumenty vedly na
stejnou hodnotu? V našem případě se to přeloží takto: Je možné, abychom ve
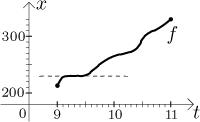
dvou rozdílných časech dostali stejné číslo? V grafu se to vidí následovně:
Existuje nějaká vodorovná čára, která by protla graf ve více než jednom bodě?
V našem případě je odpověď na všechny tyto otázky "ano", protože tam máme
malý kousek grafu, který je "plochý", asi jsme na chvíli zastavili a nehýbali
se, takže pozice zůstala stejná pro mnoho hodnot času. Z grafu bychom třeba
odhadli, že dva rozdílné časy 9.2 a 9.3 vedly oba na stejné číslo, 230.
Matematicky,
Má tato funkce inverzi? Připomeňme, že inverzní funkce
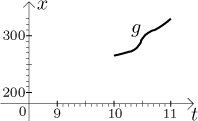
Což nás přivádí k poslednímu pojmu. Tatáž věta také říká, že funkce prostá inverzi má. V matematice má často smysl obejít problém s prostotou tak, že se ignorují "nevhodné" části funkce. U naší funkce je problém s plochou částí, můžeme se tedy soustředit na menší kousek grafu, neboli budeme uvažovat restrikci funkce f na nějakou menší množinu. Můžeme se například soustředit jen na náš výlet mezi 10 a 11. Dostaneme tak novou funkci, budeme jí říkat g, abychom si je nepletli.
Standardní značení pro restrikci vypadá takto:
Slovy, funkcí g míníme fukci získanou tak, že uvažujeme tu část funkce
f, která odpovídá argumentům z intervalu
Protože g je prostá, můžeme najít její inverzi. Například z grafu lze odhadnout, že
g(10) = 265, g(10.2) = 270, g(10.5) = 295 , g(10.8) = 315, g(11) = 330.
Inverzní funkce má proto hodnoty
g−1(265) = 10, g−1(270) = 10.2, g−1(295) = 10.5, g−1(315) = 10.8, g−1(330) = 11.
Protože inverzní funkce bere jako argumenty hodnoty původní funkce, vyplývá z toho, že definiční obor inverzní funkce je roven oboru hodnot funkce invertované. Podobně je obor hodnot inverzní funkce tvořen argumenty funkce původní, tj. jejím definičním oborem. Tato dvě fakta platí obecně, zde máme
Graf inverzní funkce dostaneme prohozením os argumentů a hodnot, neboli převrácením obrázku okolo hlavní diagonály:
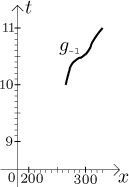
To uzavírá přehled nejdůležitějších vlastností reálných funkcí.
Poznámka o inverzi: Ve většině učebnic se inverzní funkce značí
Například v našem příkladě přijímá inverzní funkce
Když tedy píšeme
Tento příklad použijeme znovu, až budeme probírat význam derivace, a zase při vysvětlování Základní věty kalkulu.
Vrátíme se na začátek k problému pohybujícího se auta. Začali jsme tím, že
nás zajímá, kolik jsme ujeli. Mohli bychom to brát jako další funkci, řekněme
d, a
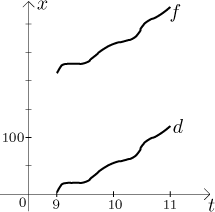
Díky tomu krásnému vzorci teď znalost f znamená, že známe i d a
naopak, a tak vlastně víme všechno. Kolik jsme například ujeli mezi
Obě funkce d a f měřily samotný pohyb. Často ale máme informaci
o pozici namísto uražené dráhy. Můžeme si například představit, že výlet byl
po důležité cestě, podél které jsou kilometrovníky. Řekněme, že jsme začali u
tabulky říkající "17 km" a skončili u tabulky "134 km". To souhlasí s
předchozím příběhem, nevraceli jsme se a výlet nám zabral 117 km. Protože se
pohybujeme pouze po silnici, jsme v jednorozměrné situaci a kilometrovníky
určují jednoznačně naši polohu. Ve fyzice se pozice v čase t obvykle
značí
Pokud nás pouze zajímá, kolik jsme ujeli, pak je
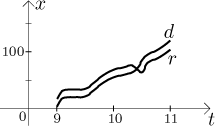
Co se ale stane, když z nějakého důvodu jedeme někdy zpátky? Kilometrovníky zaznamenané naší funkcí se začnou zmenšovat, ale cestovali jsme, takže vzdálenost d by se měla zvětšovat! Zatímco tachometr se nedá ošálit, poziční funkce přestane být přímým zdrojem pro náš výpočet vzdálenosti. To ukazuje, že dokud cestujeme jedním směrem, jsou pozice a uražená vzdálenost v zásadě stejný kus informace, ale obecně ne. I tak ale existuje způsob, jak dostat dráhu z pozice. Měl by stačit selský rozum: Stačí identifikovat extrémy cesty (místa, kde jsme obraceli) a jednoduchým odečtením zjistíme, kolik jsme mezi těmito body ujeli (mezi každými dvěma obrátkami jedeme jedním směrem, takže pozice dá vzdálenost). Tyto částečné dráhy se pak sečtou.
Obecně potřebujeme více informací, jmenovitě ke svázání pozice a dráhy je třeba derivace. Zajímavou shodou okolností, když uvádíme derivaci v části Derivace - Teorie - Úvod, použili jsme právě tento příklad, abychom ukázali její vztah k fyzice, mimo jiné jsme ukázali, že derivace dává rychlost. Pokud se na tu poznámku chcete podívat, než budete číst dále, klikněte sem. Budeme tedy předpokládat, že derivaci známe. Tento příklad jsme také použili v této poznámce, kde jsme našli spojení mezi derivací a integrálem. Usoudili jsme tam, že uražená vzdálenost se dostane z rychlosti vztahem
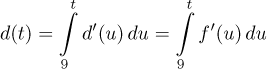
Druhá rovnost plyne z toho, že f a d popisují stejný pohyb,
jsou jen vzájemně posunuty, a proto musí derivace (rychlosti) souhlasit,
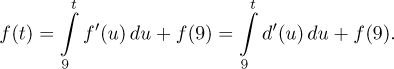
Podobně lze dostat pozici z fyzikální rychlosti (orientované) vzorcem
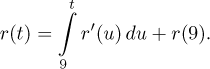
Protože běžná rychlost je absolutní hodnota z rychlosti fyzikální
(orientované), což je derivace
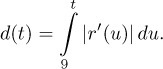
Našli jsme tedy vztah mezi pozicí r a dráhou d.