Interpretace derivace, Leibnizovo značení

Zrození derivace a diferenciálního počtu vůbec je fascinující příběh, který najdete v mnoha knihách. Měl dva otce, Newtona a Leibnize, jejichž následovníci se ještě dnes hádají, kdo je opravdový otec. Newton se k tomuto pojmu dostal přes fyziku, prostě to potřeboval, tak si to vymyslel. Říkal tomu jinak, ale myšlenka už tam byla. Značení, které zavedl, dodnes přežívá např. ve fyzice (viz níže). Je trochu podobné značení, které používáme my, ale to pochází od Lebesguea.

Leibniz k tomuto pojmu přišel z pohledu matematiky (trochu jako my v předchozí sekci), takže také přišel s jiným značením. Jak už to tak bývá, tato dvě značení, f ′ a Leibnizovo vysvětlené níže, se dnes používají jak v matematice, tak ve fyzice a dalších vědách, každé má své výhody i nevýhody a používáme to, které je zrovna lepší. Na to se podíváme v druhé části této sekce.

V poslední části se krátce podíváme na některá další značení používaná hlavně ve fyzice.

Interpretace derivace (fyzika a spol.)

Začneme v následující situaci. Jedeme autem, uvažujme funkci f (t) popisující naši pozici v čase t měřenou tachometrem (viz tento příklad pro další detaily). Uvažujme pevný čas a. Co znamená derivace f v a?

Vezměme nějaké x > a a uvažujme podíl

V čitateli máme f (x) − f (a), což je rozdíl pozic vzhledem k tachometru. Jinými slovy, říká nám to, jakou dráhu jsme urazili mezi časy a a x. Ve jmenovateli máme x − a, tj. uplynulý čas. Vzdálenost dělená časem dává průměrnou rychlost. Rozmyslete si, že když zvolíme x < a, tak bude interpretace stejná.

Vidíme tedy, že derivace je limita průměrných rychlostí přes menší a menší časové intervaly okolo našeho času a. Zdá se tedy přirozené, že derivace dává okamžitou rychlost v čase a.

Rychlost znamená rychlost změny, takže tato úvaha platí nejen pro f jako pozici (dráhu), ale pro libovolnou kvantitu. Pokud je derivace kladná, tak se měřené množství zvětšuje, pokud je derivace záporná, pak se zmenšuje. Takovéto úvahy jsou velice užitečné zejména ve fyzice. Například jsme právě viděli, že derivace pozice je rychlost. Stejně tak derivace rychlosti je rychlost její změny neboli zrychlení. Když to dáme dohromady, vidíme, že druhá derivace pozice je zrychlení. Takto se k derivaci dostal Newton.

Tyto úvahy lze také aplikovat na funkci f jako takovou, coby matematický objekt bez nějakého vztahu k fyzice nebo jiným aplikacím. Pokud si představíme graf f, pak nám derivace říká, jak rychle jde nahoru nebo dolů. Tohle je už ale větší téma, které si zaslouží vlastní kapitolu, Průběh funkce.

Značení derivace, které se používá nejčastěji a které jsme uvedli v definici, pochází od Lagrange. Jsou ale i jiná značení, Lebnizovo je v popularitě těsně druhé.

Leibnizovo značení pro derivaci funkce f (x) je

Pokud chceme také ukázat bod, kde se derivace bere, dáme jej jako (a) za ten symbol. Jako obvykle je také možné použít značení se svislou čárou (viz Úvod do reálných funkcí).

Kde se Leibnizovo značení vzalo? Počátečním bodem je otázka aproximace. Máme funkci a známe její hodnotu v bodě a. Rádi bychom věděli, jak moc se funkce změní, když proměnnou o kousek pohneme. Jeden přirozený způsob aproximace takové změny je použít tečnu:

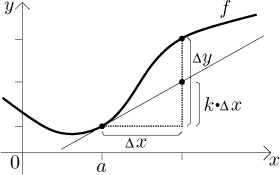
Když pohneme proměnnou o Δx, pak se hodnota funkce změní o Δy. Pokud je změna Δx malá, pak neuděláme velkou chybu, když opravdovou změnu hodnoty Δy nahradíme výrazem k⋅Δx, kde k je směrnice tečny v a.

Otázka rozumné aproximace se tedy dá převést na otázku nalezení směrnice tečny. Můžeme ji nějak najít pomocí trojúhelníků naznačených v obrázku?

Dvě věci se zdají z obrázku jasné. Za prvé, když uděláme Δx opravdu velice malé, pak je podíl Δy/Δx velice blízký ke k; na druhou stranu také vidíme, že nikdy nedostaneme k přesně, leda že bychom měli Δx = 0, ale pak ten zlomek nemá smysl.

V téhle chvíli přijdeme se zvláštním nápadem a uvedeme na scénu "nekonečně malý kousek osy x" zvaný dx. Tento podivný objekt není číslo, ale "něco", co je menší než všechna kladná čísla, přesto to ale není nula. Samozřejmě že takové podivné zvířátko neexistuje, ale když si představíme, že ano, dostaneme z toho zajímavé věci.

Když posuneme proměnnou x o "diferenciál" dx, pak se odpovídající hodnota f změní o diferenciál dy ve směru osy y. Nejdůležitější je, že když posouváme o dx namísto o Δx, pak je změna v proměnné nekonečně malá a graf funkce ještě neměl čas se začít kroutit a zatáčet; jinými slovy, vypadá v tom místě jako přímka. V důsledku toho dostaneme směrnici tečny jako dy/dx. Protože se změna v hodnotě f dá také označit jako df, dostaneme dvě možná značení:

První značení odkazuje na funkci f samotnou. Druhé značení používáme, pokud dáváme určitý důraz nebo význam na druhou proměnnou y = f (x).

Poznamenejme, že pro každou osu nemáme jen jeden diferenciál. Diferenciály jsou nekonečně malé, ale liší se velikostí. Konec konců, derivace může mít mnoho různých hodnot podle toho, jaká je funkce, což ukazuje, že diferenciál dy může být podle situace menší či větší. Vlastně je to tak, že "hodnotový" diferenciál dy není nikdy jen tak sám, vždy je spojen s funkcí a s bodem, kde pracujeme; co nás obvykle zajímá nejvíc je vzájemné porovnání velikostí dy a dx.

Pokud budeme předpokládat, že diferenciály mají smysl, pak si s nimi můžeme trochu víc pohrát a dostaneme zajímavé věci. Pokud například roznásobíme tu rovnost výše, dostaneme

Tento vzorec je zásadní v situacích, kdy měníme soustavu, ve které pracujeme, neboli když měníme proměnné. Pokud jsou nová proměnná y a původní proměnná x spojeny transformací y = f (x), pak nám ten vzorec říká, jak se transformují diferenciály. To je velice užitečné například v integrálech, viz tato poznámka.

Podobně řetízkové pravidlo vypadá úžasně snadno, když se napíše pomocí Leibnizova značení. Na konci oné kapitoly o operacích dokonce najdete další roztomilý příklad, jak Leibnizovo zančení způsobí, že věci vypadají naprosto jasně. Pro některé další situace, kde "diferenciály" zjednoduší situaci, se podívejte na tuto poznámku. Poznamenejme, že při integrování se lidem obvykle nechce blbnout s fontama, a tak píšou dx namísto správného dx, ale je to totéž.

Samozřejmě největší problém s tímhle přístupem je, že nekonečně malé kousky neexistují. Věci nicméně dlouho fungovaly zdánlivě velice dobře a lidé ty kousky používali volně a radostně, ale pak postupně zjistili, že z toho dostávali věci, které nejsou pravda. Bylo jasné, že je třeba udělat kalkulus pořádně a rigorózně, aby se dalo na jeho výsledky spolehnout. Kvůli tomu jsme nakonec skončili s epsilony a deltami, nikdo je opravdu nemá rád, ale nic lepšího se nevymyslelo. Mnoho matematiků (a fyziků atd.) si ale stejně pořád při přemýšlení nad problémy hrají s dx, protože je to velmi intuitivní, a když dojdou k nějakým závěrům, tak je pak potvrdí korektním epsilon-deltovým způsobem.

Jaké jsou výhody Leibnizova značení? Jedna výhoda je, že ukazuje, vzhledem ke které proměnné derivujeme. Některé funkce mají parametr a někdy není hned jasné, které písmenko je proměnná a které parametr. Leibnizovo značení v tom udělá pořádek. Další výhoda se ukáže za situace, kdy chápeme derivování jako určitou proceduru, která dělá něco funkcím. Bylo by pěkné mít pro takovou proceduru jméno, Leibnizovo značení jedno nabízí.

Můžeme tedy například psát

Poznámka: "Alternativní analýza" je matematická teorie, která definuje dx jako skutečný matematický objekt a vyvíjí pravidla pro práci s ním. Pak můžeme používat diferenciály a pokud dodržujeme ta pravidla, jsou všechny závěry platné. Bohužel, připravit základy pro tento přístup (definice a zkoumání dx) není snadné, takže to zůstává jednou ze zajímavých, ale málo používaných částí matematiky.

Protože fyzika byla hlavní inspirací pro kalkulus a fyzici často derivace používají, není překvapivé, že přišli s dalšími způsoby zápisu.

Značení tečkou. V reálných situacích často mícháme proměnné, které označují prostorové souřadnice, a jednu speciální proměnnou označující čas (typicky t). Protože hrají rozdílné role, má smysl použít rozdílné značení pro derivaci, aby se dále podtrhnul rozdíl. Zatímco obvyklé značení "apostrofem" se používá pro derivaci vzhledem k prostorovým souřadnicím, derivace vzhledem k času se značí tečkou (nebo více tečkami) nad písmenem. Derivace funkce x(t) by se značila

Mimochodem, tohle je značení, které pro derivaci (jakoukoliv, nejen časovou) používal Newton. Je pěkné, že přežívá alespoň takto, aby nám připomínala jednoho z autorů derivace.

Značení v subskriptu. Poznamenali jsme, že jednou z výhod Leibnizova značení je, že ukazuje proměnnou. Jenže je také docela komplikované na psaní, zvlášť pokud hodně derivujete. Máme tedy další značení, f_x označuje derivaci f vzhledem k proměnné x. Podobně jestli má f proměnnou y, zapsali bychom derivaci jako f_y.

Podívejte se do sekce o derivaci vyššího řádu, jak se zapíšou pomocí těchto alternativních značení.

Elementární derivace
Zpět na Teorie - Derivace: Úvod