Derivace: Úvod

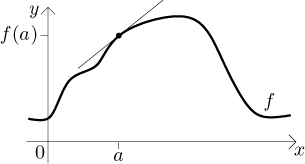
Zde nejprve zavedeme derivaci v bodě. Pak se podíváme na derivaci jako funkci a ukážeme několik základních vlastností. Nakonec se podíváme na jednostranné derivace.

K pojmu derivace dojdeme velice přirozeně, když si položíme následující otázku: Uvažujme bod (a, f (a)) na grafu funkce f. Můžeme nakreslit tečnu tohoto grafu v daném bodě?

Pro začátek uvažujme pěkný případ, funkci, která vypadá hladce a existuje na nějakém okolí daného bodu. Intuice naznačuje, že by tam měla být tečna.

Abychom našli rovnici této tečny, potřebujeme dva údaje. Jeden bod nám dali, jako druhý údaj použijeme směrnici této přímky. Jak ji najdeme? Potřebujeme nějaký přístup, který by nám umožnil dělat výpočty (chceme přesnou odpověď, takže nakreslit graf a odhadnout směrnici není vyhovující). Zkusíme následující postup.

Vezmeme nějaké číslo x blízké k (ale ne rovné) a a uvažujme přímku, která jde skrz body (a, f (a)) a (x, f (x)).

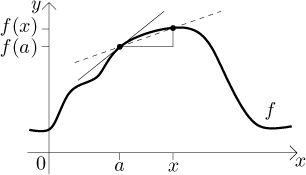
Směrnici této přímky snadno spočítáme pomocí naznačeného trojúhelníku jako

Rozmyslete si, že tento vzorec dává směrnici také v případě, že x je nalevo od a. Samozřejmě, směrnice, kterou jsme dostali, není stejná jako směrnice tečny. Pokud je ale x opravdu velice blízko k a, pak máme velice dobrou aproximaci. Když si navíc představíme, že posuneme x "úplně" k a, pak intuitivně cítíme, že by odpovídající směrnice měly dát směrnici tečny.

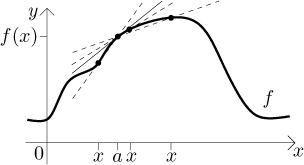
Když ale mluvíme o posunování x k a, pak vlastně mluvíme o limitě. Teď jsme připraveni na definici.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu a. Definujeme derivaci f v a vzorcem

pokud tato limita konverguje.
Jestliže konverguje, řekneme, že funkce je diferencovatelná v a.

Úvahy v úvodu teď mohou být vyjádřeny následovně:

Fakt.
Nechť f je funkce definovaná na nějakém okolí bodu a. Jestliže je diferencovatelná v a, pak existuje tečna ke grafu f v a a její směrnice je rovna f ′(a).

Příklad: Zkusíme najít tečnu ke grafu funkce f (x) =  v a = 1.

Abychom viděli, zda tam tečna je, zkusíme vypočítat derivaci v 1.

Limita konverguje, takže máme derivaci v 1 a tudíž také máme tečnu ke grafu odmocniny v 1. Má směrnici 1/2 a jde skrz bod (1,1), takže má rovnici

(y − 1) = (1/2)⋅(x − 1),

což můžeme napsat například takto: 2y = x + 1.

Derivace ovšem zahrnuje mnohem více než jen tečny, vlastně celá tato kapitola je věnována věcem, které jdou s derivací udělat, takže další zajímavé příklady necháme do dalších sekcí. Zde se podíváme blíže na derivaci jako pojem a položíme pár základních otázek.

Za prvé máme alternativní vzorec pro derivaci, který je v některých výpočtech pohodlnější.

Ekvivalence obou definic je jasná, prostě jen přeznačíme první obrázek; formálně se dá změnit jedna limita v druhou pomocí substituce x = a + h.

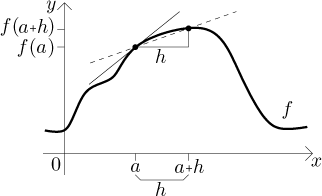
Za druhé, existence derivace je silnější pojem než spojitost:

Opačně to ale neplatí, ne každá spojitá funkce je diferencovatelná.

Příklad: Uvažujme funkci f (x) = |x| (absolutní hodnota) v bodě a = 0. Limita, která může dát derivaci, je

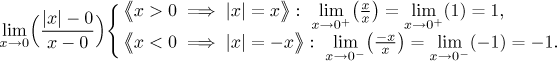
Limita neexistuje, proto není absolutní hodnota diferencovatelná v nule. Když se podíváme na obrázek, tak to vypadá rozumně, protože nemáme rozumného kandidáta na tečnu v počátku.

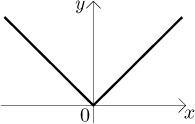
V sekci o spojitosti v části Funkce - Teorie - Reálné funkce jsme viděli, že když máme funkci spojitou v jednom konkrétním bodě, tak to ještě neznamená, že ta funkce bude "pěkná". Totéž platí o derivaci. V sekci Dirichletova funkce v části Funkce - Teorie - Elementární funkce je podivná funkce, která je v nule diferencovatelná, ale nikde jinde už není hladká, dokonce ani v grafu nemá žádné nepřerušované části. Abychom z diferencovatelnosti dostali něco rozumného, musíme se podívat na diferencovatelnost na intervalu, což je následující část.

Definice.
Uvažujme funkci f a podmnožinu G jejího definičního oboru. Řekneme, že f je diferencovatelná na G, jestliže je diferencovatelná v každém bodě G.

Připomeňme, že abychom měli v nějakém bodě derivaci, musí f existovat na nějakém okolí. Proto obvykle uvažujeme diferenciabilitu na otevřených množinách.

Uvažujme funkci f diferencovatelnou na nějaké otevřené množině G. Pak pro každý bod a z G máme derivaci f ′(a), což je nějaké číslo. Tímto způsobem tedy dostaneme předpis, který přiřazuje čísla všem bodům z G, jinými slovy dostáváme funkci.

Definice.
Nechť je funkce f diferencovatelná v každém bodě otevřené množiny G. Pak definujeme funkci derivace f na G jako funkci f ′ danou předpisem a ↦ f ′(a) pro a z G.

Příklad: Uvažujme funkci f (x) = . Největší otevřená množina, na které je definovaná, je (0,∞). Podobně jako předtím ukážeme, že pro a > 0,

Takto dostaneme novou funkci na (0,∞). Protože je zvykem používat pro proměnnou x, můžeme právě nalezený výsledek zapsat jako

Proces diferencování (derivování) tedy můžeme chápat jako proceduru, která mění funkce v jiné funkce; tato procedura splňuje užitečná pravidla, na které se podíváme v sekci Derivace a operace. Umožní nám hledat derivace algebraicky (tj. pomocí algoritmu využívajícího základní slovník a gramatiku), což je mnohem snažší než vyhodnocovat limity. Pro informace odkazujeme na onu sekci.

Poznamenali jsme, že diferencovatelnost v jednom konkrétním bodě ještě nemusí znamenat, že je funkce "pěkná". Teď máme diferencovatelnost na množině, což je mnohem mocnější vlastnost. Připomeňme, že pokud je funkce spojitá na intervalu, pak jejím grafem musí být nepřerušovaná křivka; pořád ale ještě může mít "rohy" neboli ostré ohyby. Jestliže je ale tato funkce na onom intervalu také diferencovatelná, pak musí být graf "hladký", bez ostrých rohů. Tím opět naznačujeme, že existence derivace je silnější než jen spojitost. Příslušnou lokální větu je teď možné formulovat globálně.

Věta.
Jestliže je funkce diferencovatelná na nějaké otevřené množině, pak je na ní i spojitá.

Opačně to ale zase neplatí, ne každá spojitá funkce je diferencovatelná.

Všimněte si, že se spojitost nedá protáhnout do koncových bodů. Pokud máme funkci, která je diferencovatelná na intervalu (a,b), tak ještě nemůžeme říct nic o spojitosti (jednostranné) v bodech a nebo b. Konec konců, všimněte si, že pokud yměníme hdnoty této funkce v bodě a (nebo v b), pak to nemá na derivovatelnost na (a,b) žádný vliv, viz Věta o střední hodnotě v části Teorie - Věta o střední hodnotě.

Než se vydáme dále, uděláme poznámku ohledně definičního oboru funkce derivace. Abychom měli derivaci, musíme mít nejprve původní funkci, takže evidentně definiční obor f ′ musí být podmnožinou definičního oboru f. Pojem definičního oboru tedy závisí na situaci. Například funkce 1/x má za definiční obor množinu všech reálných čísel s výjimkou nuly. Uvidíme ale také, že 1/x je derivace ln(x), který povoluje pouze kladná čísla. Proto definiční obor 1/x v situaci, kdy tuto funkci používáme jako [ln(x)]′, bude jen (0,∞).

V části Funkce - Teorie - Reálné funkce - Spojitost jsme uvedli Vlastnost mezihodnoty. Máme následující fakt.

Věta.
Jestliže je funkce diferencovatelná na nějakém otevřeném intervalu, pak tam má její derivace má vlastnost mezihodnoty.

V oné sekci jsme tvrdili, že spojité funkce mají na intervalech vlastnost mezhodnoty, teď máme další skupinu funkcí, které ji mají. Poznamenejme, že tyto dva typy nejsou shodné. I když to možná zní divně, tak jsou funkce, u kterých existuje derivace, která ale není spojitá, viz např. sin(1/x) v části Funkce - Teorie - Elementární funkce.

Definice.
Nechť f je funkce definovaná na nějakém okolí bodu a. Řekneme, že f má nevlastní derivaci v a, jestliže limita

existuje a je nevlastní.

Jaký je smysl takové derivace? Geometricky to znamená, že tečna grafu v tomto bodě je svislá. Derivace nekonečno znamená, že v tom bodě funkce roste, derivace mínus nekonečno ukazuje na funkci jdoucí dolů.

Příklad: Uvažujme funkci f (x) = x^1/3 (třetí odmocnina) v a = 0. Derivace je

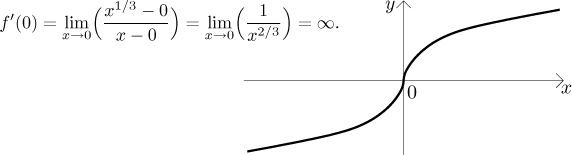
Takže ať už se s limitou v derivaci stane cokoliv, teď už víme, co to znamená. Co ještě se může pokazit s derivací? Hned ten první předpoklad, že f existuje na nějakém okolí a. Tohle se může pokazit mnoha způsoby, příliš mnoha na to, abychom v tom mohli dělat rozumný systém. Je ale jeden případ, který je tak užitečný, že si zasluhuje vlastní definici. Jmenovitě stojí za to se podívat na "jednostranné tečny" v koncových bodech definičních oborů.

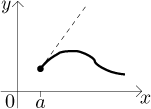
Například před chvílí jsme zkoumali derivaci druhé odmocniny na (0,∞), ale její definiční obor také zahrnuje 0. Kdybychom znali tečnu v 0 zprava, pak bychom věděli, jak správně nakreslit graf, tj. jakým směrem se vydat, když vyrážíme z 0.

Definice.
Nechť f je funkce definovaná na nějakém pravém okolí bodu a. Definujeme derivaci zprava f v a vzorcem

pokud limita konverguje.

Nechť f je funkce definovaná na nějakém levém okolí bodu a. Definujeme derivaci zleva f v a vzorcem

pokud limita konverguje.

Příklad: V příkladě s absolutní hodnotou výše jsme vlastně spočítali, že f '₊(0) = 1 a f '_-(0) = −1. To by nemělo překvapit, když vezmeme v úvahu graf absolutní hodnoty.

Jednostranná derivace má stejné vlastnosti jako ta obvyklá, všechny věty využívající derivace fungují také pro derivace jednostranné, jen se musí upravit závěry na jednostrannou situaci. Například:

Věta.
Jestliže je funkce v nějakém bodě diferencovatelná zprava, pak je tam i spojitá zprava.
Jestliže je funkce v nějakém bodě diferencovatelná zleva, pak je tam i spojitá zleva.

Opačně to zase neplatí.

Jak by se dalo čekat, "oboustranná" informace se dá dostat z jednostranných.

Věta.
Funkce f je diferencovatelná v nějakém bodě a tehdy a jen tehdy, pokud tam má derivaci zprava i zleva a ty se rovnají. Pak také f ′(a) = f '₊(a).

Nebo f ′(a) = f '_-(a), co se vám hodí víc, v této situaci jsou stejné.

Obvykle raději hledáme jednostranné derivace jako limitu derivace spíš než podle definice, viz Derivace a limita v části Teorie - Věta o střední hodnotě.

Můžeme také definovat jednostranné nevlastní derivace. Spíš než formální definici (která je teď už stejně jasná) raději ukážeme příklad.

Příklad:

Toto ukazuje, že jestli chceme nakreslit graf druhé odmocniny pořádně, musíme začít směrem nahoru ze začátku v nule.

Interpretace derivace, Leibnizovo značení
Zpět na Teorie - Derivace: Úvod