Monotonicity of real functions

Here we will introduce the notion of monotonicity. It comes in two flavours, as a local notion and a global notion. Local notions give information about properties of functions at a given point and its immediate surroundings, it does not allow one to say anything about the function further from this point. That's where we start, we cover monotonicity at a point and local extrema. Global properties look at functions as a whole. We look at global monotonicity and global extrema. Oftentimes one can use local information to derive global info out of it and vice versa, but each point of view can offer information that the other does not.

Here we will look at monotonicity from theoretical point of view, practical approach using derivatives can be found in the section Monotonicity in Derivative - Theory - Graphing functions.

Monotonicity at a point, local extrema

Given a function f and a point a from its domain, one can look at f around a and compare values with f (a). There are essentially four useful cases.

Definition (local monotonicity).
Let a belong to the domain of a function f.

We say that f is increasing at a if there is a neighborhood U of a such that for all x from U ∩ D( f ) the following is true:

•   If x > a, then f (x) > f (a),
•   if x < a, then f (x) < f (a).

We say that f is non-decreasing at a if there is a neighborhood U of a such that for all x from U ∩ D( f ) the following is true:

•   If x > a, then f (x) ≥ f (a),
•   if x < a, then f (x) ≤ f (a).

We say that f is decreasing at a if there is a neighborhood U of a such that for all x from U ∩ D( f ) the following is true:

•   If x > a, then f (x) < f (a),
•   if x < a, then f (x) > f (a).

We say that f is non-increasing at a if there is a neighborhood U of a such that for all x from U ∩ D( f ) the following is true:

•   If x > a, then f (x) ≤ f (a),
•   if x < a, then f (x) ≥ f (a).

What is the meaning of these definitions? We look at the first one. First of all, the definition is local. It starts by saying that there is a neighborhood of a on which some condition holds, no information outside this neighborhood is relevant. There is also no guarantee concerning the size of this neighborhood, it might be extremely small, which may sometimes cause problems. So now we will look at the neighborhood and see what is happening there. We start at a, where the function has value f (a). When we look at f to the right from a, the function gets larger. When we look to the left, the function gets smaller. It should then seem natural that f is called increasing at a.

The second case is similar, we just also allow the function to be equal to f (a) on U. The next two cases are exactly the opposite tendency for f. Here are typical examples of these notions:

Note that increasing automatically implies non-decreasing, and decreasing automatically implies non-increasing. Also, increasing and decreasing cannot be true at the same time. On the other hand, it is possible to have a function that is simultaneously non-decreasing and non-increasing at some point. A function that is constant on a neighborhood of some point satisfies both these properties there.

Note that we cannot expect any tendency or nice properties at other points than a, not even in the neightborhood U. Here is a relatively tame example of a function non-decreasing at a,

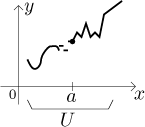
but things can get much worse. In "Saw-like" functions in Theory - Elementary functions we show an example of a function that is increasing at a certain point but there is no neighborhood of this point on which this function would be monotone or continuous.

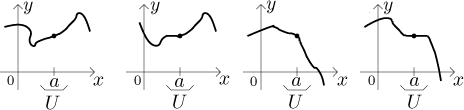
So the best one can say based on local monotonicity is that on some neighborhood of a, the graph of the function must stay in appropriate "quadrants centered at (a, f (a))" as suggested in the picture, on the left is the idea of increasing and non-decreasing, on the right the idea of decreasing and non-increasing.

Important note.
Unfortunately, this terminology is not generally accepted. Some people would not use the names increasing, non-decreasing, decreasing, non-increasing, but instead they would say (in the same order) strictly increasing, increasing, strictly decreasing, decreasing. Both terminologies have about the same number of followers and equally persuasive arguments, so it is hard to take sides. Generally, people pass on what they learned from their teachers, which is what I am doing here, I also think that single-word names are a bit better and the names we defined here are more fitting :-). Usually this is not a problem, but notice that people who use this other notation would have to also make changes in some theorems. That's where it gets confusing a bit, but fortunately it does not happen too often. The usual advice: Check what terminology your prof is using and stick to it.

Another note.
It is also possible to ask about one-sided local monotony. For instance, to be increasing at a from the right, one would have to find a right reduced neighborhood U of a such that f (x) > f (a) for all x from that right reduced neighborhood; recall that a right reduced neighborhood is an interval of the form (a,b) for some b > a. Similarly one defines other notions from the right and from the left.

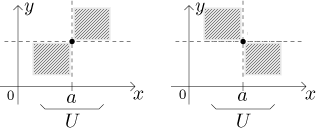
Recall the picture with quadrants above. It can also happen that when we restrict the function to a suitable neighborhood, its graph stays in certain quadrants, but they are not of the form (when going from left to right) "below-above" or "above-below" as we saw above. What are the other alternatives? There are two, "below-below" and "above-above".

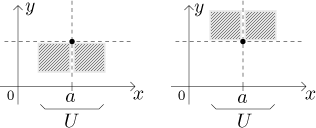
Typical examples (when the function is very nice) are

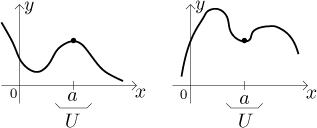
Since the "hump" and the "dip" show that the function is a bit extreme at the point a, the name "extreme" seems in place, and since we only have information about a small neighborhood, it is local.

Definition (local extrema).
Let f be a function defined on some neighborhood of a point a.

We say that f has a local maximum at a, or that f (a) is a local maximum of f, if there is a neighborhood U of a such that for all x from U ∩ D( f ) the following is true:

f (x) ≤ f (a).

We say that f has a local minimum at a, or that f (a) is a local minimum of f, if there is a neighborhood U of a such that for all x from U ∩ D( f ) the following is true:

f (x) ≥ f (a).

The name local extreme is a general handle for a local maximum or a local minimum. Some people also distinguish sharp local extrema, which basically means that they exclude the constant situation. Definition of a sharp local maximum is just like local maximum above, only the inequality is taken sharp; similarly for sharp local minimum.

Again, this is a local notion, so having a local extreme, we have no guarantee that the function behaves reasonably around that point, not even in the neighborhood U.

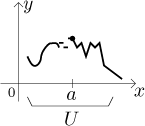
Can a point be at the same time a local minimum and a local maximum? Sounds strange but yes, if the function is constant on a neighborhood of this point.

Here we will look at the function as a whole, on some subset M of its domain. Typically, M would be an interval (including an infinite one) or a union of intervals.

Definition (global monotonicity).
Let M be a subset of the domain of a function f.

We say that f is increasing on M if for all x,y from M satisfying x < y we have f (x) < f ( y).

We say that f is non-decreasing on M if for all x,y from M satisfying x < y we have f (x) ≤ f ( y).

We say that f is decreasing on M if for all x,y from M satisfying x < y we have f (x) > f ( y).

We say that f is non-increasing on M if for all x,y from M satisfying x < y we have f (x) ≥ f ( y).

We say that f is monotone on M if it satisfies one of the above four conditions.
We say that f is strictly monotone on M if it is increasing on M or decreasing on M.

These conditions are actually quite simple. For increasing functions, when we move right, the function must go up. For decreasing functions it must go down. The "non" versions are similar, but we also allow the function to stay the same for a while.

This notion does not really make too much sense unless the set M is reasonable, typically a non-degenerate interval or a union of such intervals. Here are three typical examples of monotone functions on an interval; the first function is increasing, the second is non-decreasing, and the third is decreasing. The fourth function is not monotone on the indicated interval.

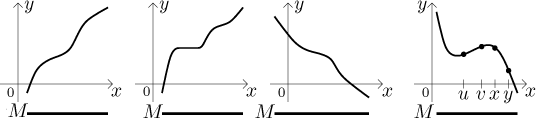
Recall that the conditions in the above definition are of the form "for every couple x, y..." and in order to violate such a condition, it is enough to find one counter-example, that is, a pair of points that do not satisfy the relevant condition. In the fourth example we indicated a pair x, y which is a counter-example to that function being increasing or non-decreasing; indeed, when going from x to y, the function does decrease and thus violates the two relevant inequalities. We also marked a pair u,v which can serve as a counter-example to the function being decreasing or non-increasing, because when going from u to v, the function does increase.

Note again that increasing automatically implies non-decreasing, and decreasing automatically implies non-increasing. Increasing and decreasing are mutually exclusive notions. However, there are functions that are simultaneously non-increasing and non-decreasing on M - namely all constant functions on M.

Important note.
Just like in the local case, this terminology is not generally accepted. Some people would not use the names increasing, non-decreasing, decreasing, non-increasing, but instead they would say (in the same order) strictly increasing, increasing, strictly decreasing, decreasing. The good news is that these people use monotone and strictly monotone just like we do, so if these notions are used in a theorem, it works for both terminologies.

Depends on what monotonicity we have. Clearly, if f is increasing on one interval and decreasing on another interval, then it cannot be monotone on the set formed by their union (draw a picture). The only interesting case is when we have the same kind of monotonicity on both intervals. We will now look at the following situation: Imagine that we know that f is increasing on I and increasing on J. Is there any monotonicity on the set obtained by their union? This is a very good question, in particular because students find it very boring to write two monotonicities as we wrote them and they tend to write it like this: "f is increasing on I ∪ J". Unfortunately, very often this is wrong and students lose points for this. Here's one such example, in the picture on the right we show two points that are a counter-example to f being increasing on the union as one set.

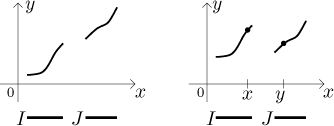
We are getting to the first important point of this part: If you write it as we did before, "f is increasing on I and increasing on J", it will be always correct. If it seems too long, try "f is increasing on I and on J". Unless you are forced to look closer, leave it this way.

But what if we really want to know more, for instance if we are asked for "maximal intervals of monotonicity"? First, there is one simple rule: If the two intervals intersect, then we do get monotonicity on their union, since the intersection serves as a nice bridge from one part of the graph to another. What if they are disjoint as on the picture above? The picture suggests what should be done. We should somehow compare values on the adjacent ends of intervals and make sure that they do not jump the wrong way. We get the following rules:

Let an interval I be to the left from an interval J, in particular they are disjoint.
1. If f is non-decreasing on I and non-decreasing on J, and sup_I( f ) ≤ inf_J( f ), then f is non-decreasing on I ∪ J.
2. If f is increasing on I and increasing on J, we have sup_I( f ) ≤ inf_J( f ) but max_I( f )=min_J( f ) is not true, then f is increasing on I ∪ J.
3. If f is non-increasing on I and non-increasing on J, and inf_I( f ) ≥ sup_J( f ), then f is non-increasing on I ∪ J.
4. If f is decreasing on I and decreasing on J, we have inf_I( f ) ≥ sup_J( f ) but min_I( f )=max_J( f ) is not true, then f is decreasing on I ∪ J

Draw a few pictures to convince yourself that these statements make sense. They are a bit complicated, since we have to take into account both open and closed situations, but in fact it is all just a common sense, in practice it is much easier than the precise (and a bit undigestible) mathematical statements here.

Local and global: relationship.

If the set M is just some general subset of the domain of the given function f, there is little hope of relating local and global monotonicity. However, once we pass to one interval, things become nice.

Theorem.
If f is a function monotone on an interval, then it is monotone (in the same way) at all interior points of this interval.

If this interval includes some of its endpoints, then at such points we have one-sided monotonicity, but this notion is rarely used, so we did not put it in the theorem. Now we try it the other way.

Theorem.
If f is a function monotone in the same way at every point of an open interval, then it is monotone (in the same way) on this interval.

Why "open"? Because the opposite of the previous theorem (where we allowed just any interval) would not work. Indeed, the function in the following picture is increasing at all interior points of the indicated interval, but it is not increasing on that interval (try going from a to any other point of that interval and the function will drop).

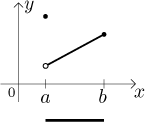
We can fix this problem by requiring one-sided monotonicity at endpoints, but this notion is rather obscure and most people never heard of it. Therefore the preference goes to a slightly weaker but way more practical statement that uses continuity:

Theorem.
If f is a function that is monotone in the same way at every interior point of an interval, and continuous on the whole interval, then it is monotone (in the same way) on this interval.

Note that continuity on an interval including endpoints actually does include a one-sided notion, but continuity from the right/left is a standard notion, so this is no problem.

Now we will look at how monotonicity helps with other properties.

So the limits at the endpoints exist, but they might be infinite.

Theorem.
If a function is strictly monotone on a set, then it must be necessarily 1-1 there and the corresponding inverse is also monotone (in the same way).

If we also have continuity and work on an interval, then this implication becomes an equivalence.

Theorem.
Let f be a function continuous on an interval I. Then f is 1-1 on I if and only if it is strictly monotone on I. If it is so, then the corresponding inverse function is also continuous and monotone on its domain.

All these notions - local and global monotonicity, local extrema - can be investigated very conveniently using derivatives, which is explained in the section Monotonicity in Derivative - Theory - Graphing functions.

We know that when we consider a function f on a set M, we can find its supremum and infimum over this set, and if we are lucky, we can also find its maximum and minimum over this set (see Basic properties). Maximum a minimum are global extrema over that set. While we had a close relationship between local and global monotonicity, with extrema it is a bit more complicated. For instance, in this example we have a local minimum and a local maximum, but there is no global maximum and the global minimum is not local minimum.

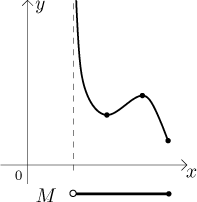
In fact, there is some interplay between local and global extremes.

Theorem.
Let f be a defined on a bounded closed interval I. If f attains its global extreme at a point c, then either f has a local extreme at c or c is an endpoint of I.

However, this still does not imply that there actually are some global extrema. Is there any way to guaarantee it? We do have one useful theorem.

Theorem (Extreme Value Theorem, EVT).
Every function continuous on a bounded closed set attains its maximum and minimum over this set.

We now look closer at this theorem. First of all, the theorem is an implication, we may have global extrema even in other cases. In the following picture we have a function that is not continuous, but it does have global extrema over a set that is not bounded nor closed. Incidentally, the picture also shows that we can have more global extrema, they need not be unique.

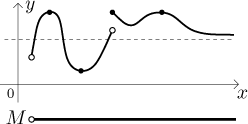
The theorem lists the necessary conditions without which global extrema are no longer guaranteed and having them is a matter if luck as in the previous picture. Now look at the following picture:

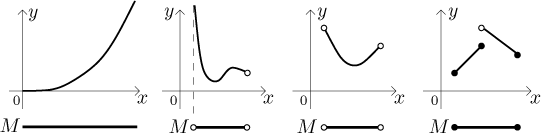
The picture on the left shows that a function that is continuous on a closed interval need not have a maximum, the boundedness is missing sorely. The next three pictures have all bounded intervals, but they have other problems. The two pictures in the middle have open intervals but no maxima, although the the middle right function is actually bounded. This shows that without closedness we also cannot guarantee anything. The picture on the right shows that even with bounded closed intervals we cannot win if we lack continuity. So we need all three properties, just two of them won't be enough.

For practical approach to determining lglobal extrema we refer to Global extrema in Derivatives - Theory - Applications.

Concavity of real functions
Back to Theory - Real functions