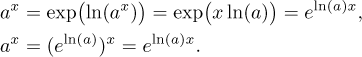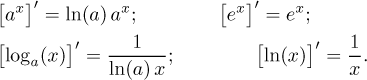Exponenciály, logaritmy

V první sekci jsme se dívali na mocninu A^B coby číslo a pak jsme z ní udělali funkci tak, že jsme zafixovali B a nechali A měnit. Teď to zkusíme naopak, pevně zvolíme A a označíme to a, abychom to zdůraznili, pak dáme x coby proměnnou místo B. Jaký bude definiční obor funkce, kterou takto vytvoříme? Abychom to zjistili, musíme trochu přeorganizovat svá pozorovnání z první sekce; tam jsme se na mocninu dívali z pohledu B, ale teď na ony závěry budeme muset nahlížet z pohledu A, tedy a.

Jestliže a > 0, pak za B můžeme dát libovolné reálné číslo. Dostaneme tedy pěknou funkci a^x. Jestliže a = 0, můžeme zase brát libovolné reálné číslo B, dostaneme tak konstantní funkci 0^x = 1 (včetně případu 0⁰ = 1). Tato funkce nicméně nebývá počítána mezi funkce, které tady zkoumáme, protože se velmi liší. Z téhož důvodu sem nepočítáme ani a = 1, protože 1^x = 1. Jestliže a < 0, pak za B můžeme brát pouze zlomky s lichými jmenovateli. Množina těchto čísel (i když je na reálné ose hustá) je velmi roztříštěná a neobsahuje žádný interval. Funkce s takovým definičním oborem je z pohledu analýzy v zásadě na nic, protože většina metod vyžeduje funkci definovanou na nedegenerovaných intervalech a jejich sjednocení. Proto také nebudeme uvažovat a < 0.

Shrnuto, definujeme obecnou exponenciálu pouze pro a > 0, a ≠ 1.

Definice.
Obecná exponenciála se základem a > 0, a ≠ 1, je funkce a^x.
Názvem exponenciála označujeme funkci e^x, kde e je Eulerovo číslo 2.718281828...

Někdy také namísto e^x píšeme exp(x) nebo Exp(x), zvlášť pokud je v argumentu komplikovanější výraz.

Číslo e musíme nějak definovat. Nejobvyklejší definice je pomocí limity, Eulerovo číslo je definováno jako limita posloupnosti (1 + 1/n)ⁿ, viz Posloupnosti - Teorie - Důležité příklady.

Obecná exponenciální funkce má jako definiční obor všechna reálná čísla. Algebraické vlastnosti mocnin nám dají pár užitečných vlastností obecné exponenciální funkce, pro všechna reálná x,y a c platí

a^x + y = a^x⋅a^y;       a^c⋅x = (a^x)^c = (a^c)^x.

Obecná exponenciála je monotonní, jmenovitě rostoucí pro a > 1 a klesající pro a mezi 0 a 1. V obou případech je obecná exponenciála konvexní. Mezi obecnými exponenciálami je přirozené uspořádání. Nerovnost a < b implikuje a^x < b^x pro x kladné a b^x > a^x pro x záporné.

Grafy vypadají takto:

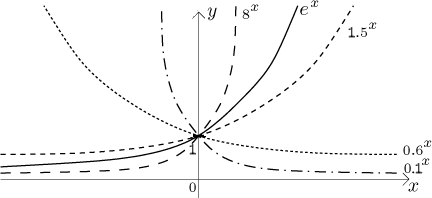
Vidíme, že obor hodnot je R(a^x) = (0,∞). Jestliže a > 1, pak

Pro a∈(0,1) máme

Pro a > 0, a ≠ 1 je obecná exponenciála a^x na svém definičním oboru monotonní funkce a tedy prostá. Má proto inverzi. Tato inverzní funkce se nazývá logaritmus se základem a a značíme ji log_a(x). Přesně, pro x kladné definujeme log_a(x) jako číslo y splňující a ^y = x.

Speciální případ, když a = e, se jmenuje přirozený logaritmus a značí se ln(x). Inženýři také používají logaritmus o základu a = 10, říká se mu dekadický logaritmus a obvykle se značí log(x).

Vlastnosti logaritmu přirozeně plynou z vlastností exponenciály. Máme dvě důležité algebraické identity:

log_a(x⋅y) = log_a(x) + log_a(y);       log_a(x^c) = c⋅log_a(x).

Mimochodem, ačkoliv mnoho studentů mívá během písemek divokou fantasii, bohužel opravdu neexistuje žádná identita pro log_a(x + y).

Definiční obor logaritmu je (0,∞), obor hodnot je celá reálná osa a log_a(1) = 0. Logaritmus je monotonní -- rostoucí pro a > 1, klesající pro a∈(0,1) -- a konkávní. Důležité limity v koncových bodech jsou pro a > 1 tyto:

a pro a∈(0,1) tyto:

To je ostatně vidět z grafů:

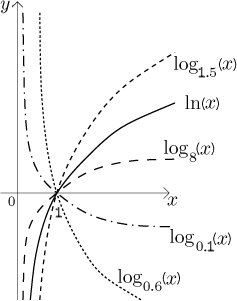
Zase máme přirozené srovnání, ale tentokráte je drobet komplikovanější a závisí na tom, jak se základ porovná s 1. Jestliže a < b < 1 nebo 1 < a < b, pak log_a(x) < log_b(x) pro x∈(0,1) a log_b(x) < log_a(x) pro x > 1. Jestliže a < 1 < b, pak log_b(x) < log_a(x) pro x∈(0,1) a log_a(x) < log_b(x) pro x > 1.

To, že logaritmus je inverzní funkce k příslušné obecné exponenciále, se dá vyjádřit těmito důležitými rovnostmi:

x = log_a(a^x) pro x reálné     a     x = a^log_a(x) pro x > 0.

Druhá rovnost vyžaduje jen trochu přemýšlení a ta první je ještě snažší, ukážeme to dvěma způsoby:

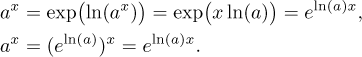
Uzavřeme tuto sekci vzorci pro derivace:

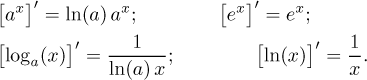
Zajímavá poznámka: Existuje několik způsobů, jak definovat exponenciálu. Matematici mají rádi abstraktní věci, proto často používají tuto verzi:

Exponenciála je funkce f definována na reálné ose, která splňuje f (0) = 1, f ′(0) = 1 a f (x + y) = f (x)⋅f (y) pro všechna x,y.

Je samozřejmě třeba dokázat, že taková funkce existuje jen jediná, ale to se dá udělat, a protože naše exponenciála vyhovuje těmto podmínkám, musí to být ona funkce. Podobně se dá definovat obecná exponenciála změnou druhé podmínky na f ′(0)=ln(a).

Obecná mocnina
Zpět na Teorie - Elementární funkce