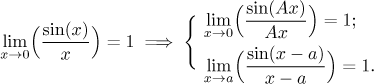
Je to metoda, která může pomoci s vyhodnocením některých limit. Dá se na ni nahlížet jako na jednoduchý trik, ale je také možné kolem ní vyprávět příběh, což nás přivádí k názvu. To slovo "infinitesimála" rozhodně neodkazuje na infinitesimálu dx známou z derivování či spojitosti dle Leibnize. Význam je jiný a vysvětlíme jej níže. Nejprve se podíváme na ten snadný přístup.
Následující limita je velmi známá, pomocí substituce z ní pak snadno odvodíme další verze:
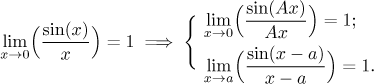
Můžeme je použít k zjednodušení dalších limit následujícím způsobem (ukážeme to velmi detailně, abychom ten postup ospravedlnili):
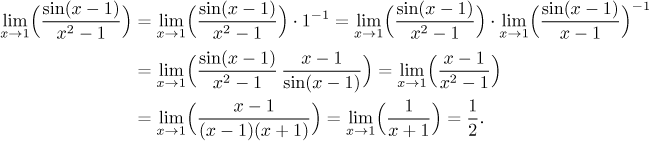
Porovnejte první limitu s tou poslední na druhém řádku. V zásadě jsme sinus
nahradili výrazem
Věta.
Nechť je a reálné číslo, ∞ nebo−∞. Nechť f, g, h jsou funkce definované na nějakém prstencovém okolí a. Jestliže
pak
Poznamenejme, že situaci, kdy podíl dvou funkcí
f a h konverguje k 1 v a, jsme už probrali v sekci
řád funkce a uvedli jsem tam
následující značení:
• Jestliže
Povšimněte si omezení na typ výrazu. Obecně vzato se nedá nahrazovat kdekoliv, jak uvidíme níže.
Často počítáme limity v
Zde je seznam populárních ekvivalentních infinitesimál.
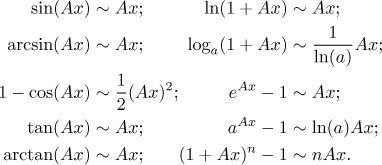
Poznamenejme, že to n v posledním vzorci může být libovolné kladné reálné číslo, například zlomek. Vzorec tedy pomůže i s odmocninami.
Příklad: Následující limitu vyřešíme pomocí ekvivalentních infinitesimál.
![]()
To bylo znatelně snažší než použití l'Hospitalova pravidla. Ve škole (u zkoušky) to ale můžeme dělat jen v případě, že byly v předmětu ekvivalentní infinitesimály řádně zavedeny.
Vzorce výše také pomohou s limitami v jiných bodech než nule pomocí vhodných substitucí.
Příklad:
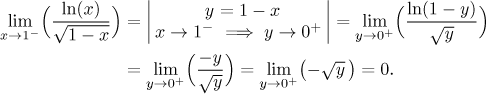
Příklad:
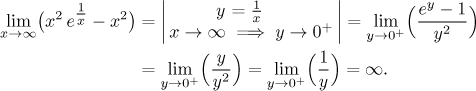
Hlavní omezení této metody je, že bezpečně lze nahrazovat jen za čitatel či jmenovatel jako celek. Stačí se podívat na následující příklad.
Příklad:
![]()
Tento výsledek je špatně, správná odpověď je
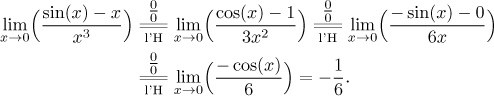
Při pohledu na tabulku ekvivalentních infinitesimál je možné si všimnout, že ve všech případech je výraz napravo přesně prvním členem Taylorova rozvoje funkce nalevo. Není to náhoda. Obecně lze při výpočtu limity v bodě a nahrazovat funkce jejich rozvoji se středem v a. Pokud použijeme plný rozvoj (mocninnou řadu), tak to můžeme dělat kdekoliv chceme, pokud dotyčná mocninná řada konverguje k původní funkci na nějakém okolí a.
Práce s řadami ale není vždy snadná. Často je lepší použít jen nenulový Taylorův polynom jistého stupně. Pak musíme být opatrní, abychom neudělali chybu. Určitě to můžeme udělat, pokud funkce, kterou nahrazujeme, tvoří čitatel či jmenovatel zkoumaného zlomku. Pokud chceme nahrazovat jinde, pak je třeba zvolit stupeň tak, abychom neztráceli klíčovou informaci. Intuitivně řečeno, můžeme nahradit část zkoumaného výrazu jejím Taylorovým rozvojem určitého stupně, pokud se následně tento rozvoj zcela nezkrátí. Toto samozřejmě není přesná matematická podmínka, bylo by obtížné dát přesný a vyčerpávající popis vzhledem k tomu, jak rozličné mohou limity být. Když se rozhodnete nahrazovat, je důležité tomu dobře rozumět a mít dost zkušeností s limitami.
Jako příklad se vrátíme k výpočtu, který nám nahoře selhal. Ukážeme to dvakrát. Začneme pozorováním, že při pokusu o nahrazení sinu polynomem prvního stupně došlo k jeho vykrácení, tudíž byl moc krátký. Zkusíme proto hned následující možnou délku, tedy polynom třetího stupně, jehož část by už v čitateli měla přežít.
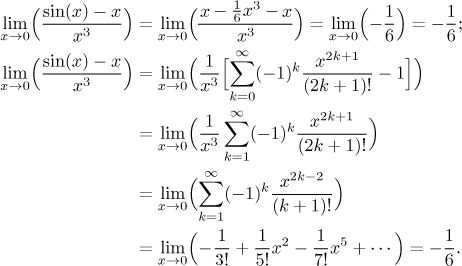
Protože se ekvivalentní infinitesimály běžně neprobírají, nebudeme je v Math Tutoru používat v oficiálních řešeních.