Intuitivní výpočet

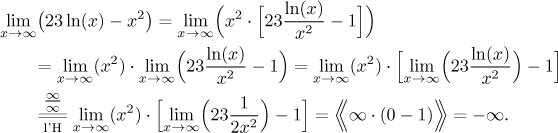
Zde se pokusíme uhádnout limitu funkce v nekonečnu, samozřejmě také ukážeme, jak takový odhad potvrdit. Podíváme se na funkce, které obsahují různé typy mocnin (polynomy, exponenciály) a logaritmy, přesnější popis uvedeme níže.

Poznamenejme, že některé z našich úvah by také fungovaly pro limitu v mínus nekonečnu, ale je to tam občas zrádné. Existuje jednoduchý trik, který to pro nás udělá bezpečně: Je-li dána limita v mínus nekonečnu, pomocí substituce ji změníme na limitu v nekonečnu a všechny triky z této sekce se dají použít.

To hádání, které zde probereme, je velice užitečné a obvykle nabízí nejkratší řešení pro výrazy, které by se jinak musely dělat jinými způsoby, často pomocí l'Hospitalova pravidla vedoucího ke komplikovaným výrazům. Používají se dvě základní ingredience. První je dobrá znalost algebry limit, obzvláště základních limit, druhá důležitá složka je dobré pochopení vzájemného vztahu mocnin a exponenciál (a odmocnin). Začneme krátkým úvodem.

V mnoha funkcích máme součty mocnin a podobných výrazů. Uvažujme například funkci x³ + 5x^1/2 − x⁻², zajímá nás její limita v nekonečnu. První dvě mocniny jdou do nekonečna (kladná mocnina), třetí mocninu si lépe přepíšeme jako 1/x², což konverguje k 0. Pomocí algebry limit teď snadno najdeme limitu celé funkce: ∞ + 5⋅∞ − 0 = ∞.

Teď se podívejme na tento příklad: Jaká je limita v nekonečnu funkce f (x) = x³ − 5x²? Víme, že ∞ − ∞ je neurčitý výraz. Máme postupy k nalezení výsledku, ale příslušné metody občas vedou ke komplikovaným výpočtům. V této sekci se naučíme, jak uhádnout správnou odpověď a jak ji snadno (v zásadě) dokázat.

Mimochodem, když sčítáme a odčítáme nějaké objekty a dokonce je násobíme reálnými čísly, jak jsme teď dělali, říkáme tomu "lineární kombinace". Výraz v tomto příkladu byl tedy "lineární kombinace mocnin". Tuto terminologii budeme v této sekci používat. Nejprve zkusíme přesně napsat, jaký problém nás tu zajímá.

Všimněte si, že záporné mocniny ve výrazech jako nahoře nepůsobí problémy, viděli jsme, že x⁻² jde v nekonečnu k nule a proto v algebře limit nedělá problémy, když se přičte k něčemu jinému. V této skci proto budeme uvažovat pouze kladné exponenty. Pokud jsou všechny tyto exponenty náhodou celá čísla, pak vlastně mluvíme o polynomu. Budeme ale pracovat obecněji a připustíme i necelé kladné exponenty (například exponent 1/2 neboli odmocnina).

Povolíme také "exponenciály", tedy mocniny tvaru a^x. Zde zase víme, že a^x→0 v nekonečnu jestliže a < 1 a 0 zde není problém, takže budeme uvažovat jen exponenciály a^x s a > 1.

To ale není všechno. Zatímco se "lineární kombinace" mocnin a exponenciál jak popsáno (mocniny/exponenciály násobené čísly a sčítané/odčítané) objevují často, přidáme ještě další výrazy: logaritmy a dokonce mocniny tvaru x^x. Teď jsme připraveni formulovat problém, který tu budeme řešit:

Otázka:
Máme výraz ve tvaru α⋅A(x) + β⋅B(x) +..., kde funkce A(x), B(x),... mohou být mocniny x^a s a > 0, exponenciály a^x s a > 1, mocniny logaritmů [ln(x)]^a s a > 0 a obecné mocniny jako x^x. Co se s tímto výrazem stane, jestliže pošleme x do nekonečna?

Všimněte si, že všechny výrazy vypsané výše jdou do nekonečna pro x→∞. Když je spojíme v lineární kombinaci, v typickém případě dostaneme nějaký neurčitý výraz s nekonečny, protože odpověď dostaneme rovnou jen v případě, kdy se ta nekonečna sčítají. Co když se odčítají? Brzy uvidíme, že některá nekonečna jsou "větší" než jiná.

Řešení problému:
Jestliže necháme x→∞, pak výraz uvedený výše se bude chovat přesně jako jeho dominantní člen. Aby se to dokázalo matematicky, vytkne se dominantní člen z výrazu a pak se aplikuje limita. Výraz, který zůstane po vytknutí, by měl jít k nenulovému reálnému číslu.

"Dominantním členem" míníme člen který - pro velká x - převáží nad všemi ostatními členy v dané lineární kombinaci, takže je možné ty ostatní členy ignorovat a nebudou zasahovat do tendence, kterou má dominantní člen okolo nekonečna. Mezi typy vypsanými výše (mocniny, exponenciály, logaritmy,...) existuje hierarchie. Když řekneme "člen A převáží nad členem B pro velké hodnoty x", tak tím opravdu míníme, že když zkoumáme limitu výrazu α⋅A + β⋅B pro x jdoucí do nekonečna, pak můžeme ignorovat člen B a starat se jen o A. Zde jsme záměrně trochu nepřesní a drobet mlžíme, protože chceme ukázat jednoduchý a praktický přístup; toto téma lze zpracovat i pořádně matematicky a je spojené s dalšími pojmy, pokud vás to zajímá, podívejte se na následující sekci o řádu funkcí.

Příklad:
Brzy uvidíme, že x² převáží nad ln(x) v nekonečnu. Teď si představte, že potřebujeme najít limitu 23ln(x) − x² v nekonečnu. Když se x stává opravdu velkým, druhý člen převáží a první můžeme ignorovat. Výraz se tedy bude chovat (pro x rostoucí do nekonečna) jako výraz -x², o kterém víme, že jde do mínus nekonečna. Proto také daný výraz jde do mínus nekonečna.

To jsme ale samozřejmě jen hádali. Nahoře (v Řešení) jsme napsali, že matematicky to uděláme vytknutím dominantního členu. Zkusíme to:

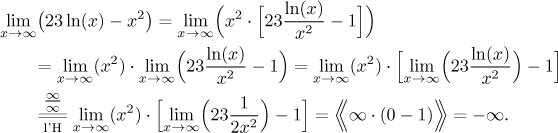
Všimněte si, že člen, který vznikl po vytknutí dominantní mocniny, opravdu šel k nenulovému reálnému číslu, přesně jak bylo řečeno. Ta nenulovost je pak podstatná pro algebru limit, nemůže vzniknout ∞⋅0.

Existuje způsob, jak zapsat naše intuitivní úvahy pořádně. Když napíšeme A(x) ∼ B(x), míníme tím, že výrazy A a B se chovají stejně pro x→∞; z praktického pohledu jsou výrazy A(x) a B(x) stejné pro x opravdu velmi velké. Říkáme také, že A a B jsou "stejného řádu". Ta intuitivní úvaha výše se dá napsat i takto:

23ln(x) − x² ∼ −x²→−∞.

Poznamenejme, že tento pohodlný způsob zápisu není univerzálně přijímán. Nepředstavuje také pořádné řešení - konec konců jsme jen hádali. Jakákoliv odpověď, kterou takto dostaneme, musí být ověřena korektním matematickým výpočtem, například tím vytýkáním, které jsme ukázali výše.

Když se díváme na mocniny v lineární kombinaci mocnin a dalších podobných členů, děláme vlastně dvě různé věci. Nejprve se podíváme jen na mocniny, exponenciály atd, tedy ignorujeme multiplikativní konstanty před nimi. Tímto způsobem určíme typ výrazu. Například výraz "13⋅[ln(x)]³" je typu [ln(x)]³ a ten příklad výše je typu x², protože typ je dán typem dominantní mocniny. Typ nám řekne, jakou zhruba rychlostí výraz "utíká" pro opravdu velká x.

Tento typ používáme, když zhruba porovnáváme chování různých výrazů, hledáme, které členy lze ignorovat atd. Když pak opravdu hledáme limitu v nekonečnu, musíme do našich úvah také zahrnout multiplikativní konstantu. Řekli bychom tedy, že 23ln(x) − x² je typu x² pro x jdoucí do nekonečna, ale když se pak snažíme uhádnout limitu v nekonečnu, měli bychom říct, že je řádu -x²; jinými slovy při proceduře ∼ musíme zachovávat i konstanty.

Jak vidíte, intuitivní postup může být snadný, zapsat to pořádně matematicky (vytknutím) je možná delší, ale nemělo by to být trikové - pokud tedy správně identifikujeme a vytkneme dominantní člen. Což nás přivádí k hlavnímu tématu této sekce:

Zde je seznam výše zmíněných členů od nejvíce dominantního k nejméně. Jinak řečeno, každý jmenovaný člen převáží nad těmi, které jsou jmenovány po něm:

(1)   mocnina x^x,
(2)   exponenciála a^x pro a > 1,
(3)   mocnina x^a pro a > 0,
(4)   logaritmus [ln(x)]^a pro a > 0.

V praxi lidé často dávají přednost hovorovějšímu vyjádření této hierarchie, například říkají "mocniny přebijí logaritmy v nekonečnu" a "exponenciály přebijí mocniny v nekonečnu" atd. Důkazy této hierarchie jsou ukázány pro posloupnosti v této poznámce, pro funkce se to dokazuje prakticky stejně.

Když zkoumáme lineární kombinace takovýchto členů, nejprve vždy najdeme dominantní výraz. Může se ale stát, že je více výrazů dominantní kategorie. Proto také potřebujeme znát vzájemný vztah uvnitř každé kategorie. Pravidlo je tu jednoduché. V kategoriích (2), (3) a (4) je vždy nějaký parametr (tj. a) a ten nejvyšší je ten dominantní.

Otázka dominance je vlastně jednou z možných odpovědí na otázku "které z nekonečen je větší". Na následujícím obrázku (který není zcela v měřítku) jsme zkusili symbolicky vyjádřit vztah mezi jednotlivými typy výrazů, čímž jsme dostali škálu mocnin:

Příklad:
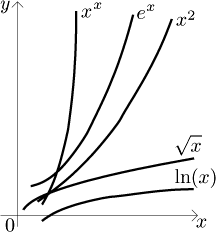
Jaká je limita 13⋅2^x + x² − 5⋅3^x − [ln(x)]^1/2 v nekonečnu?

Řešení: Máme tam tři kategorie: exponenciály, mocniny a logaritmy. Exponenciály jsou na seznamu nejvýše, takže z nich vyjde dominantní člen. Jsou dva kandidáti, 2^x a 3^x. Protože 3 > 2, ten druhý bude dominantní člen, neboli daný výraz je typu 3^x. Můžeme tedy ignorovat všechny ostatní členy a odhadnout, že

13⋅2^x + x² − 5⋅3^x − [ln(x)]^1/2 ∼  − 5⋅3^x→ − 5⋅∞ = −∞.

Jak tento odhad potvrdíme matematicky? Vytknutím dominantního členu.

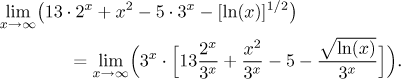
Tři zlomky v závorce se nejlépe udělají samostatně. První je jen exponenciála, druhé dva vedou na l'Hospitalovo pravidlo:

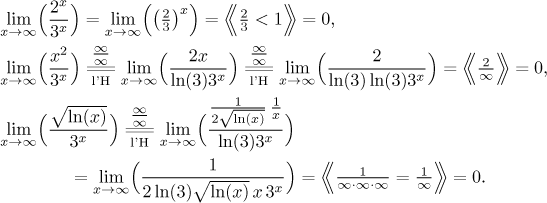
Nakonec dostáváme

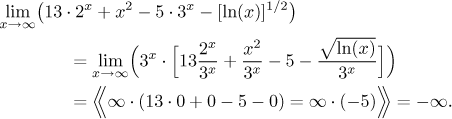
Poznamenejme, že tyto úvahy lze uplatnit i na členy, které nevypadají úplně stejně jako ty výše, ale dají se na ně převést algebraicky. Dva nejtypičtější příklady: (2x)³ = 2³⋅x³ = 8⋅x³ a 3^2x+1 = (3²)^x⋅3¹ = 3⋅9^x.

Intuitivní proces funguje také v případě, když jsou do výrazu zapleteny nějaké odmocniny; jinými slovy, některé části výrazu mohou být uzavřeny pod odmocninami. Pak děláme následující. Nejprve se podíváme na každou odmocninu zvlášť. Pro každou z nich najdeme dominantní člen výrazu uvnitř, to určí typ výrazu pod odmocninou. Když na toto aplikujeme zkoumanou odmocninu, dostaneme typ odmocniny jako celku. Toto se dá potvrdit vytknutím, zbylá odmocnina by pak měla mít v nekonečnu nenulovou vlastní limitu.

Poté, co jsme se vypořádali s odmocninami (pokud nějaké jsou), dáme všechny typy dohromady (ty, které tam už byly samotné, a typy odmocnin) a určíme, který z nich je dominantní pro celý výraz. Tuto proceduru je možné opakovat několikrát, pokud je tam odmocnina, pod kterou je výraz s další odmocninou atd. Když nakonec určíme dominantní člen celého výrazu, pokračujeme jako dříve, tj. vytkneme dominantní člen ven a podíváme se na limitu.

Poznámka: To vytýkání se většinou dělá lépe, pokud při tom opakujeme hádací postup, tj. nejprve vytkneme dominantní členy zpod odmocnin a pak se propracujeme ven.

Příklad: Najděte (pokud existuje)

Nejprve se podíváme na tu odmocninu. Jsou pod ní jen mocniny, takže patří do stejné kategorie a vyhraje ta s vyšším exponentem. V našem případě je výraz pod odmocninou typu x⁶. Když na to aplikujeme odmocninu, zjistíme, že odmocnina jako taková je typu x^6/2 = x³, přesně jako druhá část daného výrazu. Máme tedy dva členy stejného typu, dva dominantní členy, nemůžeme proto ani jeden z nich ignorovat. Zkusíme teď to hádání, nejprve budeme ignorovat člen pod odmocninou, o kterém víme, že to jde.

Dostali jsme odhad (po cestě jsme viděli, že se odmocnina sama chová jako 3x³ pro velká x) a teď to dokážeme. Začneme podle rady vytknutím dominantního členu z odmocniny.

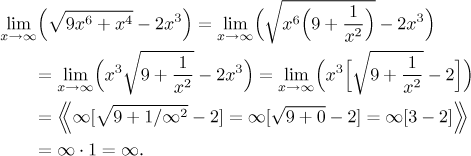
Po pravdě řečeno, to hádání nahoře mohlo být klidně špatně a ani bychom o tom nevěděli, protože jsme ještě neprobrali jednu důležitou věc. Měli jsme zatím štěstí, ale teď už je čas na

Varování: Co se stane, když máme několik dominantních členů? Pokud se sčítají, můžeme to bezpečně udělat. Pokud se odečítají (tj. pokud by algebra limit vedla na neurčitý tvar ∞ − ∞), pak musíme být velmi opatrní. Jestliže by použití obvyklé algebry na dominantní členy během hádací fáze zachovalo tento dominantní typ, můžeme to udělat jako obvykle. Jestliže by ale algebrou tento dominantní typ zmizel, nelze hádání použít!

Pokud bychom například v tom posledním příkladě měli 4x⁶ namísto 9x⁶, pak by se odmocnina chovala jako 2x³, což by se zkrátilo s tím druhým členem. Krok 2x³ − 2x³ = 0 pak není možné udělat.

Proč tomu tak je? Protože když hádáme, tak každý člen vlastně reprezentuje nejen sebe, ale možná i další členy nižší důležitosti v něm skryté (jako "9x⁶" reprezentuje i část "+ x⁴" v posledním příkladě). Když odečítáme dominantní členy a něco zbyde, pak ty části, které jsme předtím ignorovali, mohou být pořád ignorovány (dominantní člen, který je předtím zastínil, tam pořád je) a výpočet je správný. Kdyby nám ale algebrou zmizel dominantní člen, pak by byl jeden ze členů, které jsme předtím ignorovali, povýšen na dominantní, takže by teď tento dominantní člen určoval výsledek limity! V takových případech musíme použít přesnější, opatrnější postup výpočtu, který by neignoroval členy, které mohou být dočasně nedůležité.

Porovnejme následující dva příklady; možná vypadají hloupě, ale dobře ukazují, oč tu jde. U každého z nich nejprve provedeme odhad (i když to třeba bude špatně) a pak ukážeme správný výpočet.

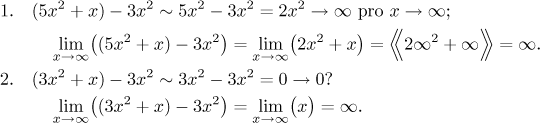
V prvním příkladě je hádání korektní; všimněte si, že při pořádném výpočtu se po sloučení členů pořád dalo ignorovat to "+ x", takže opravdu nehrálo roli pro celkový výsledek. V druhém příkladě je toto x povýšeno k dominanci.

Pravidlo pro dominantní členy: Když hledáme limitu v nekonečnu odhadem a ve výrazu je více dominantních členů, pak je můžeme slučovat algebraicky jen za předpokladu, že se tím nepokrátí.

Pokud se pokrátí, musíme opustit intuitivní výpočet a zkusit jinou metodu. I pak ale odhad často pomůže jako příprava, protože často je užitečné znát typy výrazů.

Poznámka: Mluvili jsme o odmocninách, ale to jsou jen speciální mocniny (druhá odmocnina je 1/2-tá mocnina atd). Popsaná procedura samozřejmě funguje na všechny takové mocniny, takže by nás nemělo zarazit, kdyby se ve složitějším výrazu objevil člen jako (x² − x + 1)¹³. Patřil by mezi ty, se kterými začneme, našli bychom dominantní člen vnitřku x² a celá mocnina je pak typu x²⁶.

Teď jsme se dostali k nejtypičtějšímu výrazu, který můžeme dělat intuitivními výpočty: zlomek, jehož čitatel a jmenovatel jsou typu popsaného výše. Jak s takovými zlomky pracujeme? Nejprve zvlášť prozkoumáme čitatel a jmenovatel: Určíme jejich dominantní členy a vytkneme je. Pak máme dominantní člen v čitateli a dominantní člen ve jmenovateli, takže je zkrátíme, pokud to jde, a najdeme limitu výsledného podílu. I tam nám může pomoci škála mocnin. Pokud převáží člen v čitateli, dostaneme nekonečno jako limitu v nekonečnu. Pokud převáží člen ve jmenovateli, dostaneme nulu jako limitu v nekonečnu.

To je zcela přirozené. Obvykle skončíme v situaci nekonečno nad nekonečnem, a když něco převáží, pak to znamená, že jedno nekonečno je větší než to druhé nekonečno, tudíž vyhraje. Pokud například nekonečno ve jmenovateli převáží nad nekonečnem v čitateli, znamená to, že jmenovatel je nakonec mnohem mnohem větší než čitatel, výsledný zlomek je proto velice malý, což naznačuje, že jde k nule.

Zmínili jsme, že někdy je možné zkrátit dominantní členy čitatele a jmenovatele; dostaneme pak typ zlomku jako celku.

Někdy při práci se zlomky lidé dávají přednost krácení před vytýkáním. Funguje to - ale jen někdy. Podrobnou diskuzi toho, jak zacházet s podílem polynomů v nekonečnu, nabízíme v této poznámce.

Příklad:
Najděte (pokud existuje)

Nejprve zkusíme najít odpověď intuitivně, pak to uděláme pořádným výpočtem. Začneme s odmocninami.

Pod třetí mocninou je dominantním členem třetí mocnina, pro velké hodnoty x tedy můžeme ignorovat ostatní členy. Pod druhou odmocninou ve jmenovateli převáží exponenciála nad druhou mocninou a je tedy možné tuto mocninu ignorovat.

Teď známe typy odmocnin v nekonečnu, můžeme je tedy porovnat s ostatními členy a najít dominanty, pro čitatel a jmenovatel zvlášť. Pak použijeme hierarchii mocnin k odhadnutí výsledku.

Jak jsme uvažovali? V čitateli přebijí mocniny logaritmy a nejvyšší mocnina je ta druhá. Mimochodem, toto ukazuje, proč je důležité začít odmocninami. Na první pohled by se totiž mohlo zdát, že v čitateli je dominantní x³, ale po analýze odmocniny jsme viděli, že se vlastně chová jen jako x.

Ve jmenovateli je dominantní exponenciála 2^x, takže jsme ignorovali zbytek. A nakonec jsme z toho, že v nekonečnu exponenciály pobijí mocniny, usoudili, že zlomek konverguje k nule.

Teď bychom to měli potvrdit výpočtem - jmenovitě vytknutím. Zkušený student by to urazil na pár řádcích, ale my chceme ukázat i detaily a přidat poznámku ohledně těch odmocnin; výpočty proto nabízíme zde.

I když se to nestává často, někdy se výrazy typu popsaného výše také násobí. V takovém případě se intuitivní procedura aplikuje nejprve na každý člen součinu a najde se jejich typ. Typ celého součinu je pak součinem jednotlivých typů. Většinou tak ale nedostaneme jeden z typů popsaných výše (mocniny, exponenciály atd ), spíše jejich součin. Takové výrazy nejsou součástí naší škály mocnin, zřídkakdy proto rovnou dostaneme odpověď. Často se dá ale díky zkušenosti s typy získat alespoň něco.

Příklad:

Všimněte si, že jsme zjistili, že čitatel je typu x2^x a jmenovatel je typu x²2^x; naštěstí se daly tyto dva typy chytře zkrátit a pořád jsme dostali odpověď pomocí škály mocnin. Stačí ale malá změna a už to nebude fungovat:

Teď (po zkrácení) porovnáváme dva typy x2^x v čitateli a x^x ve jmenovateli. Protože to první není částí obvyklé škály mocnin, nevíme, co se stane, když tyto typy vydělíme. Víme, že x^x přebije 2^x, ale evidentně x2^x jde do nekonečna mnohem rychleji než 2^x; mohlo by se stát, že to jde do nekonečna o tolik rychleji, aby to předběhlo i x^x, tj. je možné, že x2^x přebije x^x?

Odpověď je, že ne. Ve skutečnosti je x2^x speciální typ, který přebije 2^x a je přebito x^x, takže se vejde přesně mezi tyto dva typy. Funkce z příkladu konverguje v nekonečnu k nule; nejsnažší důkaz by byla modifikace důkazu, že faktoriál přebije exponenciály, viz Appendix v této poznámce.

Intuitivní výpočet je možné aplikovat i na komplikovanější výrazy. Bylo by komplikované vyjádřit přesně, kde všude můžeme tento typ úvah uplatnit, ale méně přesně to je takto: Základní stavební jednotkou je lineární kombinace mocnin, exponenciál, mocnin logaritmů a obecných mocnin (jejich násobky sečteny/odečteny). Tato základní kombinace se pak může strčit pod odmocninu/do mocniny, čímž vznikne nová stavební jednotka, která může být zase částí lineární kombinace. Tyto lineární kombinace lze spojovat pomocí zlomků/součinů a tak dostat nové členy pro další lineární kobinace. Všechny tyto procedury je možné opakovat v libovolném pořadí.

Varování: Zatím jsme v pohodě ignorovali části lineárních kombinací a později dokonce i odmocniny, když se staly nedůležitými ve srovnání s jinými členy. Je ale třeba být opatrný ohledně dvou věcí. Za prvé, ignorování částí je možné jen v lineárních kombinacích; odmocniny/mocniny a podíly/součiny je možné ignorovat jen poté, co jsou nahrazeny svými dominantními členy a tak se stanou povolenými součástmi lineárních kombinací. Za druhé a důležitěji, to ignorování je možné dělat pouze u výrazů typu popsaného výše (směs lineárních kombinací, odmocnin/mocnin a podílů/součinů). Není možné ignorovat části výrazů, ve kterých jsou zamíchány jiné funkce. Například je možné nahradit výraz x − ln(x) pouhým x, jestliže je to pod odmocninou nebo součástí zlomku, ale už to nemůžeme dělat, pokud je to argument řekněme exponenciály. Takže 2^x-ln(x) ∼ 2^x je špatně, sinh(x − ln(x)) ∼ sinh(x) je špatně atd.

Pro mnoho příkladů odkazujeme na Řešené příklady - Limity.

Řád funkce, asymptoty
Zpět na Teorie - Limita