The situation is as follows: We are trying to find the limit at some a
of a ratio ![]() or
or
![]() . What
can we do? There are several alternatives.
. What
can we do? There are several alternatives.
This is the standard procedure.
Step 1. Check that the ratio
Step 2. Apply the l'Hospital rule:
![]()
that is, differentiate the numerator and the denominator of the fraction.
Then try to find the limit of the resulting fraction; if this limit exists,
then it is also the answer to the original problem.
If the limit on the right does not exist, then we get no conclusion about
the original problem.
Example:
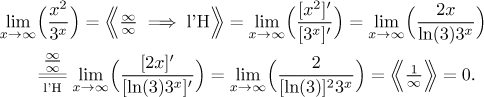
Note that we had to use the l'Hospital rule twice. This is nothing strange, if we had x13/3x, we would have to use l'Hospital's rule 13 times, each time "killing" one power of x. Most popular applications of this rule involve "killing" powers and polynomials, one can also "kill" logarithms this way.
Notes:
1. When applying l'Hospital's rule, we take separately the
derivative of the numerator and the denominator. We do not apply the ratio
rule to the whole fraction, as students are sometimes tempted to do.
L'Hospital's rule has nothing to do with taking derivative of the given
expression, it is a special
tool for finding limits that happens to use derivatives in its own way. Of
course, if the expressions in the numerator and denominator are more
complicated, we use the appropriate rules when differentiating them.
2. It is crucial to check that we are facing an indeterminate ratio (or more generally that |g| tends to infinity as x goes to a). That is, in full generality, this rule applies to two types: "zero over zero" and "anything over infinity". For other types the rule does not work, see L'Hospital rule in Theory - Limits.
3. Although the l'Hospital rule works in great many cases and seems to be quite reliable, it is not a universal solution to indeterminate ratios. Sometimes it cannot be applied at all, for instance if the functions f and/or g are not differentiable. Sometimes the l'Hospital rule can be used, but it fails to help, that is, the new limit that we obtain is no improvement. One of the possible reasons for this we will point out here: The power of l'Hospital rule lies in the "killing" power of derivative. However, some expressions do not get improved by differentiation, then l'Hospital often fails. There are two popular cases:
Exponentials are preserved. Example:
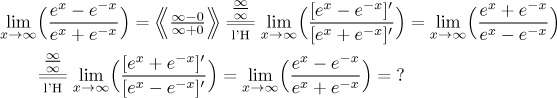
For this limit, it is better to approach it using the tools from the box
"polynomials, sums and ratios with powers at
infinity", see below. However, it might be worth the time to make the following
remark. At this point we do not know whether the limit in question exists.
But if it does, we can call it L and then the equation we got after
the first l'Hospital can be written as
Roots do not disappear after differentiation and usually get worse. Another cyclic example:
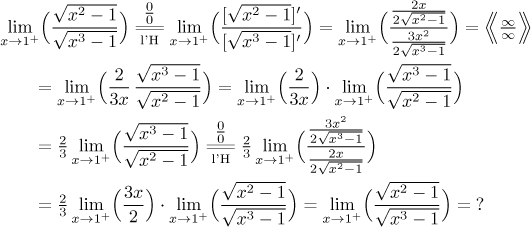
Here the easiest way out is probably cancelling:
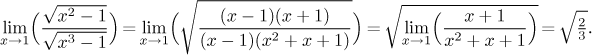
Thus for many indeterminate ratios it is better to look for alternatives.
If the limit also falls into the box "polynomials, sums and ratios with powers at infinity", we are usually better off using tools from that box. As an example we return to the one with exponentials above. In the fraction, the numerator and denumerator have the same dominant term, namely ex. The appropriate method calls for cancelling this term:
![]()
This is also sometimes possible. We saw one example above, another one is in the box "polynomials at proper points".
As we mentioned above, roots are sometimes quite troublesome when it comes to l'Hospital rule. If the roots are mixed up in a difference, they might be removed using the appropriate trick from the box "difference of roots".
Almost all examples in Solved Problems feature indeterminate ratios, so check them out.
Of course, there are also indeterminate ratios that can't be solved using these four approaches and one has to handle them individually.
Next box: indeterminate product
Back to Methods Survey
- Limits