Box "indeterminate product"

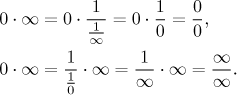
Here we will look at the following problem: We need to find a limit of the product f⋅g at some a and after trying to substitute a, we find that the product is of the type 0⋅∞.

The standard solution is to transform the product into a ratio by algebra. If we do it as outlined below, such a ratio will be of the indeterminate type and we can apply the tricks from the box "indeterminate ratio", most likely the l'Hospital rule.

How do we change a product into a ratio? We choose one of the two terms in the product and apply the "one over one over" trick to it; indeed, we know from algebra that for any non-zero A we have A = 1/(1/A). The resulting ratio will be of a type that depends on which part of the product we process this way, whether the "zero part" or the "infinity part":

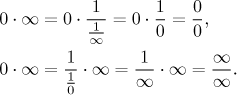
Note that in the second variant we actually cheated when we wrote that 1/0 = ∞. We know that when dividing by zero, we have to check on the type of it, and only then do some conclusions. Since we do not know whether the "0" in the product is actually one-sided, we have to be careful a bit here. If it is, we get plus or minus infinity as outlined above. What if the zero is not one-sided? If we plan on using l'Hospital's rule, then this is not a problem. Its generalized version requires that the absolute value of the denominator goes to infinity and 1/|0| = ∞ indeed.

What if we have one of those unusual problems where we cannot use l'Hospital? One possibility is to use the first version of transformation into a ratio. If that is not possible, we have a rare case that has to be handled individually. There is a trick that might help, see this note.

Still, in most cases this is not a problem.

Example:

We have an indeterminate product, so we will try to change it into a fraction. Which part do we choose to play with? There are two things to take into account. First, the part that we will play with will change, there will be an extra power to −1 composed with it, so we usually choose to play with an expression that does not get much worse (from the point of view of derivative) when we compose it with the power to −1. The second (and usually less important) factor is this: It would be also nice if the part of the expression that we leave as it is would improve after we differentiate it.

In this example the choise is therefore quite clear. We will play with the part x, since x⁻¹ is actually the same kind of expression, namely a power, so differentiating it we again get something simple, a power. The part that is left as it is, the logarithm, actually gets replaced by another power after the derivative, which is a nice bonus.

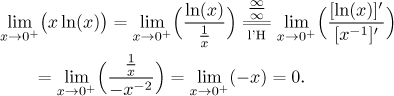
What happens if we try to play with the second part of the product? Since [ln(x)]⁻¹ is markedly worse than ln(x) from the point of view of derivative, we expect trouble.

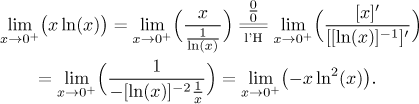
As you can see, the new expression is even worse than the one we started with, so this way it will not work. This suggests that the choice of the transformation into ratio can determine whether we succeed or not.

In Solved Problems - Limits, these methods are used in this problem and this problem.

Next box: indeterminate difference
Back to Methods Survey - Limits