Box "indeterminate difference"

Here we will address the following problem: We want to find a limit and after substituting we obtain the indeterminate expression ∞ − ∞.

There is a standard procedure, but it leads to rather ugly expressions so we will leave it as the last resort and first expore some alternatives:

Trick 1. If the two infinities involve powers, exponentials, logarithms, factorials, roots and combinations of these types, and the dominant powers of the infinities are different, then we can find the limit at infinity by factoring out the dominant term, see the box "polynomials, sums and ratios with powers at infinity".

Trick 2. If the two infinities are actually roots, we can often fix the problem by getting rid of the roots and some cancelling, see the box "difference of roots".

Trick 3. Sometimes the two "infinities" allow natural algebraic simplification into one fraction, typically in the from of some common denominator. Such ratios are very often of the indeterminate type and we can use the l'Hospital rule.

Simple Example:

Trick 4. Sometimes we can factor out some factor and get a product. If we are lucky, this product can be evaluated right away, often we would get a product of indeterminate form and we would solve it using the appropriate trick, see the box "indeterminate product".

In general, we can express it as follows: A − B = A⋅(1 − B/A). If the ratio B/A goes to 1, we get the indeterminate type ∞⋅0, otherwise we get the answer right away.

Example: The expression x³ − x² is at infinity of the type ∞ − ∞. We try to factor out the first term and obtain

x³ − x² = x³(1 − 1/x).

When we try to put in infinity, we get

∞³⋅(1 − 1/∞) = ∞⋅(1 − 0) = ∞.

In fact, note that we did exactly the factoring business from trick 1, since x³ is the dominant power at infinity.

Trick 5. We can always transform the difference into a fraction as follows:

What is the type of this new expression?

This is an indeterminate ratio. However, as you can see, the resulting fraction is quite complicated, so the calculations tend to be long and it is better to first try one of the previous tricks and use this one only as the last resort. We will try to apply this trick to the previous example.

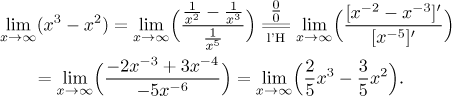
As you can see, the general trick did not help.

In Solved Problems - Limits, these methods are used in this problem and this problem.

Next box: indeterminate power
Back to Methods Survey - Limits