Parametrické funkce

Když máme křivku v rovině, ať už dánu pomocí funkce nebo implicitní rovnice, tak jsme s ní zatím pracovali jako s tvarem. Jsou ale někdy situace, kdy je v situaci víc informace, jmenovitě když je křivka vlastně záznam pohybu, dráha projitá řekněme broukem.

Pak samotný tvar nestačí, protože dva brouci mohou lézt po stejné dráze velmi rozdílnými způsoby (může se měnit rychlost i směr, je dokonce možné, že se na chvilku vrátí a jdou zpět po stejné trase). Tuto dodatečnou informaci je třeba nějak uchovat a nejpřirozenější způsob je věc zvaná parametrická křivka.

Takovou křivku získáme docela snadno. V každém čase t, o který se zajímáme, zaznamenáme pozici v rovině, její souřadnice x a y. Taková parametrická křivka je pak popsána dvěma funkcemi závisejícími na čase x = x(t) a y = y(t) pro t z nějakého intervalu I. Zde budeme vždy předpokládat, že tyto dvě funkce jsou spojité na I, takže dráha bude jedna nepřerušovaná křivka.

Takový parametrický popis již nese kompletní informaci včetně okamžité rychlosti v každém čase. Vzhledem k tomu, že brouk se může pohybovat po velmi obecných drahách, mohou být křivky popsané parametrickými rovnicemi velmi komplikované a je malá šance, že se je podaří popsat jako grafy funkcí. Můžeme se ale pokusit popsat alespoň části pomocí funkcí, abychom pak mohli použít nástroje, které už známe, hlavně naše postupy k nalezení průběhu funkce. Nejprve se ale podíváme na několik příkladů.

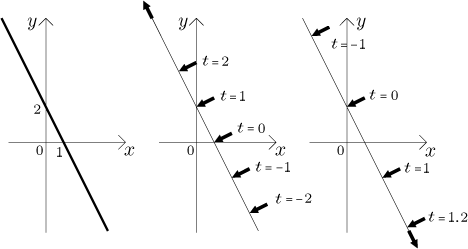
Příklad: Uvažujme parametrickou křivku
x = 1 − t,
y = 2t pro t reálné.

Jaký má tato křivka tvar? Zde je to vlastně velmi snadné, protože můžeme eliminovat parametr t. Z první rovnice dostaneme t = 1 − x, dosazením do druhé dostaneme y = 2 − 2x pro x reálné. Dráha popsaná danými parametrickými rovnicemi je tedy vlastně přímka (a to celá, pro t reálné se také x mění skrz všechna reálná čásla).

Příklad: Uvažujme parametrickou křivku
x = 2t³,
y = 2 − 4t³ pro t reálné.

Jaký má tato křivka tvar? Zde vlastně není nutné vyjadřovat z první rovnice samotné t, můžeme psát y = 2 − 2⋅2t³ = 2 − 2x. Tato parametrická křivka je tedy stejná jako ta předchozí, jediný rozdíl je v parametrizaci. Z fyzikálního úhlu pohledu tyto dvě křivky představují rozdílné pohyby,

ale z pohledu mamtematického, pokud je zkoumáme jako křivky, jde o totéž.

Příklad: Uvažujme parametrickou křivku
x = 2t²,
y = 2 − 4t² pro t reálné.

Zase máme naší přímku, ale všimněte si, že ačkoliv i teď se t mění skrz všechna reálná čísla, nemůžeme dostat záporná x. Proto je tato křivka jen část přímky y = 2 − 2x daná podmínkou x ≥ 0.

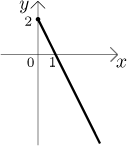
Příklad: Uvažujme parametrickou křivku
x = t⋅e^t,
y = t³ + 6t pro t ≥ −1.

Nevíme, jak vypadá, protože nedokážeme vyjádřit t z první ani druhé rovnice. Abychom získali nějakou představu o jejím tvaru, bude třeba použít nějak metody z průběhu grafů, ale na to bychom potřebovali vědět, jak takové křivky derivovat. Pro další pohled na tento příklad odkazujeme na sekci Parametrické funkce v části Derivace - Přehled metod - Průběh funkce.

Když se pokoušíme pracovat s parametrickými křivkami jako s funkcemi, narazíme na stejné problémy, jaké jsme měli s implicitními funkcemi, jmenovitě že křivka může mít vícenásobné hodnoty pro jedno x. Proto i strategie, kterou přijmeme, bude podobná. Nebudeme se pokoušet o totální konverzi, bude nám stačit lokální popis. Stejně jako u implicitní funkce máme větu o tom, že lokálně dokážeme popsat "pěkné" parametrické křivky pomocí funkcí.

Pro aplikaci této věty na příklad výše, který jsme neuměli vyřešit, viz sekce Parametrické funkce v části Derivace - Teorie - Implicitní a parametrické funkce. Zase zde máme situaci, že věta dává existenci, ale nepomůže s hledáním té funkce. V praxi buď používáme pokročilé metody hledání průběhu, nebo zkusíme eliminovat t, jak jsme to dělali výše. Jeden takový příklad je v Řešených příkladech.

Poznámky:
1. Zápis x = x(t), y = y(t) je velice výstižný, ukazuje, že souřadnice bodu závisí na čase, ale také může občas mást, zejména když y začne také lokálně záviset na x. V situacích, kde by mohlo dojít ke zmatení, lidé raději píšou x = f (t), y = g(t), pak je vše jasné.

2. Když transformujeme parametrickou křivku ve funkci, obvykle to děláme po kouskách. Vezmeme co největší kus křivky a zkusíme jej vyjádřit jako funkci, pak vezmeme kus hned vedle a zkusíme jej popsat a tak dále. Použité intervaly se objeví samy, když zkusíme vyjádřit z jedné z rovnic t (obvykle z první), protože na to potřebujeme prostotu. Jestliže je J podinterval I, na kterém je x(t) prostá, pak můžeme najít inverzní funkci t = x₋₁(x) a dosadit ji do y, tak dostaneme funkci y(x) popisující přesně tu část parametrické křivky, která odpovídá časům z J. Mimochodem, toto ukazuje, proč může být nešikovné nazývat jak proměnnou, tak funkci jako "x", vypadá mnohem lépe, když napíšeme (viz předchozí poznámka) t = f₋₁(x), pak dostaneme zásadní vzorec

y = g( f₋₁(x)).

Strategie tedy vyžaduje, abychom rozdělili I na intervaly, na kterých bude funkce f (nebo x(t) chcete-li) prostá a pak popsali odpovídající části křivky pomocí výše odvozené funkce. Protože nejjednodušší způsob, jak určit tyto intervaly, je pomocí monotonie a derivace, necháme toto téma do sekce Parametrické funkce v části Derivace - Teorie.

3. Mluvili jsme o transformaci parametrických křivek ve funkce. Funguje to i naopak? Když máme graf funkce f, můžeme jej popsat jako parametrickou křivku? Odpověď je rozhodně kladná, říká se tomu parametrizace křivky a není jednoznačná, daný graf může být vyjádřen nekonečně mnoha způsoby. Na začátku jsme například měli dvě různá parametrická vyjádření téže přímky, v druhém příkladě můžeme změnit třetí mocninu v libovolnou jinou lichou mocninu a zase dostaneme stejnou přímku. Obecně se graf f pro x z intervalu I dá přirozeně parametrizovat jako
x = t,
y = f (t) pro t z I.

Bonus: Několik slavných křivek.

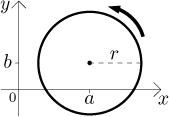
Všimněte si, že brouk obíhá opakovaně dokola proti směru hodinových ručiček nekonečně mnoho krát, a to konstantní rychlostí. Dostaneme tedy stejnou křivku, pokud změníme rychlost brouka, například můžeme použít cos(kt) a sin(kt) pro libovolné nenulové k (pro záporná k leze brouk ve směru hodinových ručiček), nebo například cos(e^t) a sin(e^t). Můžeme také zkusit jinou modifikaci. Je pro brouka zbytečné obíhat křivku vícekrát, takže můžeme ponechat vzorce, jak jsou dány, ale brát t pouze z intervalu řekněme ⟨0,2π⟩.

Elipsa s hlavní poloosou A, vedlejší poloosou B a středem (a,b) je dána rovnicemi
x = a + A⋅cos(t),
y = b + B⋅sin(t) pro t reálné.

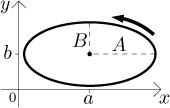
Všimněte si, že brouk leze opakovaně dokola proti směru hodinových ručiček, můžeme tedy zase omezit čas.

Poznámka: Všimněte si, že v rovnici kružnice nám parametr t vlastně určuje úhel vzhledem k ose x, pod kterým se brouk zrovna nalézá, druhá podstatná informace je vzdálenost r od středu. S touto vzdáleností si také můžeme pohrát, například ji lze nechat také záviset na čase.

Pokus zkusíme dosadit nějaké výrazné časy (jako π/4 atd.), měli bychom dostat docela dobrou představu, co se děje. Brouk leze kolem a kolem, začne v počátku a zvětšuje vzdálenost od středu konstantní rychlostí.

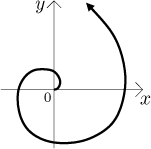
Dostali jsme Archimedovu spirálu. Pokud dáme jako poloměr jinou funkci, získáme jiné zajímavé tvary.

Poznámka: Poznamenejme, že t nemusí reprezentovat čas. Z matematického úhlu pohledu prostě máme parametr (pro který dokonce můžeme použít i jiné písmeno než t), konkrétní interpretace nemá vliv. V aplikacích může mít navíc parametr jinou roli než čas, takže když porozumíte parametrickým křivkám, je dobré se příliš neupínat na představu času (zvlášť když jsou také povrchy s více parametry, tam představa času totálně padá). Nicméně ona "časová" představa je tak přirozená a hlavně užitečná, že jsme se rozhodli na ní založit výklad parametrických křivek. Samozřejmě, i když parametr může znamenat něco jiného, všechny metody zde pokryté pořád fungují. A když se dostanete do problémů, tak můžete alespoň předstírat, že parametr je čas, a třeba to pomůže (jen to nikomu neříkejte).

Zpět na Teorie - Implicitní a parametrické funkce