Příklad: Identifikujte tvar parametrické křivky
x = e^t − 1,
y = e^2t − 2e^t pro t reálné.

Řešení: Nemá smysl používat nějaké věty, protože by (s trochou štěstí) jen zaručily lokální existenci, zatímco my potřebujeme globální a konkrétní popis. Mohli bychom zkusit standardní postup pro kreslení parametrických křivek (viz Parametrické funkce v části Derivace - Teorie - Průběh funkce nebo Parametrické funkce v části Derivace - Přehled metod - Průběh funkce), ale to by nám dalo jen náčrt, zatímco otázka říká "identifikujte". Jediná procedura, která by opravdu přesně identifikovala tvar, je změnit parametrický popis buď na funkci, nebo alespoň na implicitní rovnici, kterou už poznáme.

To se dělá eliminací t z popisu. Můžeme vyjádřit t z jedné z rovnic výše? Ta první vypadá docela dobře, tak to zkusíme. Všimněte si, že ve skutečnosti nepotřebujeme samo t, protože my to budeme chtít dosadit za t do vzorce pro y, ale tam je to t vždy jako e^t, stačí tedy vyjádřit z první rovnice tuto exponenciálu.

Rovnice y = x² − 1 definuje nahoru orientovanou parabolu, která protíná osu x v bodech −1 a 1. Tvar dané parametrické křivky je tedy dán touto parabolou, ale nemusí to být celá parabola, záleží na parametrizaci. Co se dá říct o hodnotách x a y?

Výraz x = e^t − 1 s t procházejícím všemi reálnými čísly má obor hodnot (−1,∞), protože vždy e^t > 0 a exponenciála dojde na všechna kladná čísla. Pro parametrickou křivku tedy vezmeme jen část paraboly danou nerovností x > −1.

Co druhá souřadnice? Výraz y = e^2t − 2e^t se analyzuje snáze, pokud označíme z = e^t a přepíšeme y jako y = z² − 2z neboli y = z(z − 2). Jakých hodnot tento výraz dosahuje pro z > 0? Můžeme si nakreslit graf tohoto výrazu a zjistíme, že dosahuje hodnot mezi −1 (včetně) a nekonečnem, což souhlasí s tou ořízlou parabolou, ke které jsme došli v předchozím odstavci.

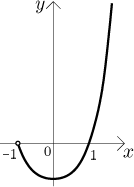
Závěr je, že dané parametrické rovnice popisují část paraboly y = x² − 1 danou nerovností x > −1.

Zpět na Řešené příklady - Implicitní a parametrické funkce