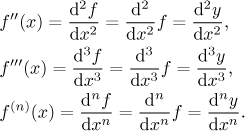
Derivace vyššího řádu, totální diferenciál

Derivace vyššího řádu je vlastně velice jednoduchá věc. Když najdeme derivaci funkce, dostaneme derivaci prvního řádu, derivaci řádu 1 nebo prostě první derivaci. Abychom dostali druhou derivaci, tak zderivujeme znovu (pokud je to možné), takže f ′′ = [ f ′]′. Podobně tím, že zderivujeme třikrát, dostaneme třetí derivaci atd. Obecně musíme k definici n-té derivace použít indukci. Kde začneme? Je vhodné začít 0-tou derivací, což je prostě f, derivujeme nula krát, tj. vůbec. Pak se ještě musíme rozhodnout, jak to zapisovat, protože by nebylo moc pohodlné zapisovat řekněme 23-tí derivaci pomocí apostrofů, také bychom tak nebyli schopni zapsat derivaci obecného řádu. Standardní značení pro n-tou derivaci je f ⁽ⁿ⁾ (pozor na ty závorky).

Definice.
Uvažujme funkci f definovanou na okolí bodu a. Definujeme nultou derivaci, také derivaci řádu 0, v a jako f ⁽⁰⁾(a) = f (a).
Pro přirozené číslo n definujeme n-tou derivaci, také derivaci řádu n, v a indukcí jako f ⁽ⁿ⁾(a) = [ f ⁽ⁿ⁻¹⁾]′(a) pokud existuje.

Jestliže n-tá derivace v a existuje, pak řekneme, že f je n-krát diferencovatelná v a.

Nechť f je funkce na otevřené množině G. Jestliže její n-tá derivace existuje ve všech bodech G, řekneme, že f je n-krát diferencovatelná na G.

Příklad: Najdeme všechny derivace f = x³ − 5x² + 13.
f ⁽⁰⁾ = f  = x³ − 5x² + 13.
f ⁽¹⁾ = f ′ = [x³ − 5x² + 13]′ = 3x² − 10x.
f ⁽²⁾ = f ′′ = [ f ′]′ = [3x² − 10x]′ = 6x − 10.
f ⁽³⁾ = f ′′′ = [ f ′′]′ = [6x − 10]′ = 6.
f ⁽⁴⁾ = f ′′′′ = [ f ′′′]′ = [6]′ = 0.
f ⁽⁵⁾ = f ′′′′′ = [ f ′′′′]′ = [0]′ = 0.
Evidentně f ⁽ⁿ⁾ = 0 pro všechna n > 3. Tato funkce f je nekonečně mnoho krát diferencovatelná na reálné ose.

Alternativní značení:
Při zápisu derivací lidé obvykle nepíšou ty apostrofy "pořádně", s tečkou a zakrouceným ocáskem, ale prostě jen udělají čárku. To lze také interpretovat jako velké I. To inspirovalo jiný zápis pro derivace vyššího řádu, jmenovitě římskými čísly. Derivace až po řád tři se píšou normálně, ale pak už můžeme psát f ′′′′ = f ^IV, f ′′′′′ = f ^V, 6-tá derivace je f ^VI, 7-má derivace je f ^VII atd.

Derivace vyššího řádu a další značení:
Leibnizovo značení:

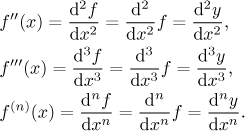
Značení tečkou (použijeme teď funkci x s proměnnou t):

Značení subskriptem:

Totální diferenciál je pojem, který vyšel z potřeby aproximovat danou funkci f lineární funkcí poblíž daného bodu a. Když má funkce jen jednu proměnnou (což je náš případ), pak má také ta lineární funkce jen jednu proměnnou a popisuje přímku. Nejlépe padnoucí přímka je tečna, takže v jedné proměnné je totální diferenciál jenom jinak oblečená tečna. Nepřináší to tedy nic opravdu nového, ale pro úplnost to tady probereme.

Definice.
Uvažujme funkci f definovanou na okolí bodu a. Totální diferenciál f v a je lineární transformace L(h), která splňuje

Značení: Totální diferenciál f v a se značí df (a), takže když dosadíme h, zapíšeme to jako df (a)[h].

Definice znamená následující. Předpokládejme, že máme totální diferenciál v a. Jestliže je x velmi blízko k a, pak by f (x) mělo být skoro stejné jako f (a) + L(x − a). Máme následující větu.

Věta.
Uvažujme funkci f definovanou na okolí bodu a. Totální diferenciál f v a existuje tehdy a jen tehdy, když je f diferencovatelná v a. Pak také

df (a)[h] = f ′(a)h.

Takže v jedné dimenzi je totální diferenciál opravdu jen derivace, ale jinak zapsaná. To je ještě jasnější, když zapíšeme totální diferenciál alternativním způsobem (který je vlastně docela rozšířený), kde použijeme diferenciál dx namísto h:

df (a)[dx] = f ′(a)dx.

Stejně obvyklá je zkrácená verze, která dává totální diferenciál ve všech bodech a (tj. na množině):

df = f ′dx.

Přesně tenhle vzoreček už jsme měli v sekci o Leibnizově značení. Proč nám tedy stojí za to se s totálním diferenciálem babrat? V okamžiku, kdy začneme uvažovat funkce více proměnných, tedy funkce žijící na vícerozměrných prostorech, tak už není nějaký rozumný způsob, kterým bychom mohli zobecnit derivaci, aby pořád měla vlastnosti, které se nám tak líbí v jedné dimenzi. Pojem totálního diferenciálu ale zobecnit jde a ukáže se, že je docela užitečný, dá se dokonce použít v abstraktnějších prostorech.

My vlastně už tu obecnou definici máme nahoře, protože můžeme celý výrok použít tak, jak je, jen s jednou malou změnou v situaci. Namísto reálných čísel coby prostoru, kde f žije, si vezmeme rozumný abstraktní prostor S, což hlavně znamená, že v tom prostoru máme nějaké lineární operace a také pojem okolí bodů. Pomocí těchto okolí pak můžeme definovat pojem limity přesně jako u reálných čísel. Definice totálního diferenciálu, kde a a h se berou z prostoru S, pak má smysl. Tohle všechno je samožřejmě pěkně vysoko nad úrovní Math Tutoru.

Derivace a operace
Zpět na Teorie - Derivace: Úvod