Příklad: Najděte derivaci funkce

Řešení: Funkce je dána vzorcem, takže derivujeme pomocí pravidel. Poslední operace, která se v daném výrazu dělá, je druhá odmocnina, tj. daný výraz je ve tvaru druhá odmocnina něčeho. Musíme tedy aplikovat řetízkové pravidlo na složenou funkci, kde vnější funkce je druhá odmocnina. Potřebujeme pravidlo pro derivaci odmocniny (hodí se to pamatovat), ale když si to nepamatujeme, odvodíme si jej pomocí elementární derivace mocniny.

Teď to použijeme s danou funkcí (která má tvar "druhé odmocniny něčeho") a řetízkovým pravidlem.

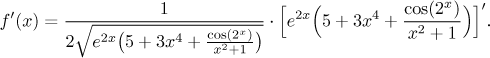
Abychom ušetřili čas a místo, nahradíme první výraz dočasně kosočtvercovou značkou a soustředíme se na tu derivaci. Poslední operace, kterou děláme při výpočtu, je násobení (derivovaný výraz je součin dvou členů), takže použijeme součinové pravidlo.

Derivace nalevo je derivace složené funkce. Použijeme řetízkové pravidlo, vnější funkce je e^y s derivací e^y, za y dáme 2x. Derivace napravo je z lineární kombinace výrazů, použijeme tedy linearitu derivace.

Vezmeme to odleva. Derivace 2x se dělá pomocí pravidla pro lineární funkci

[Ax + B]′ = A.

Totéž pravidlo pomůže s [5]′. Pak tam máme elementární derivaci mocniny a nakonec jednu složitější derivaci. Výraz uvnitř je zlomek, použijeme tedy podílové pravidlo.

Máme tam dvě derivace k vyřešení. První je z kosinu nějaké funkce, takže máme složenou funkci a podle řetízkového pravidla začneme derivací vnější funkce kosinu. Druhý výraz se derivuje snadno, podle linearity derivujeme každou část zvlášť, jedna je standardní mocnina a druhá konstanta.

Konečně jsme u konce, ta zbývající derivace je elementární.

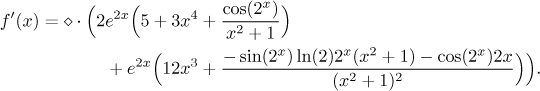
Zbývá nahradit kosočtverec příslušným výrazem a najít definiční obor této derivace. Začneme tím, že se podíváme na danou funkci, a vezmeme to zevnitř. Zlomek ve jmenovateli je vždy alespoň 1, takže tam problém není. Kosinus 2^x také akceptuje všechna reálná čísla, takže ze zlomku žádná podmínka neplyne. Zbytek výrazu pod odmocninou také nezlobí, takže zbývá zkontrolovat tu odmocninu. Potřebujeme, aby výraz v ní byl alespoň nula. To rozhodně platí pro exponenciálu na začátku, takže aby nám součin fungoval, musíme zajistit, že ten velký člen v závorce nebude záporný. To není jeden z typických problémů, které by se dělaly řešením nějaké nerovnice, na to je výraz příliš složitý. Musíme použít naši zkušenost a intuici.

Co tam tedy máme? První dva členy tvoří polynom, druhý z nich je sudá mocnina a tedy není nikdy záporný. Víme tedy, že ten polynom je vždy alespoň 5. K tomu přidáváme zlomek. Může ten být záporný? A jestliže ano, jak moc?

Jmenovatel je vždy kladný, ale čitatel a tedy i celý zlomek někdy mohou být záporné (to je škoda). Mohli bychom dostat velké záporné číslo? K tomu bychom potřebovali udělat jmenovatel velmi malým nebo čitatel velmi velký. Nicméně jmenovatel je vždy nejméně 1, zatímco čitatel je nejvíce 1 v absolutní hodnotě, máme tedy (pro všechna reálná x)

Vidíme, že daná funkce existuje všude. Teď se podíváme na derivace. Je tam nějaké nové omezení? Odmocnina by neměla být nulová, ale už jsme viděli, že je vždy nejméně 1, takže je vše v pořádku. Máme tedy

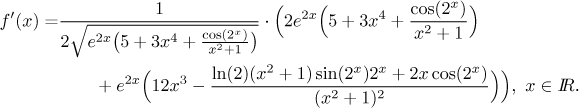
Poznámka: Pokud zapomenete derivaci z 2^x, můžete ji vždy najít pomocí triku "e na ln".

[2^x]′ = [e^xln(2)]′ = e^xln(2)[xln(2)]′ = 2^x⋅ln(2).

Další příklad
Zpět na Řešené příklady - Derivace