Příklad: Najděte derivaci funkce

Řešení: Funkce je dána výrazem, můžeme tedy najít její derivaci pomocí pravidel. Protože má tato funkce x v základě i exponentu, je to obecná mocnina. Musíme ji tedy předtím, než něco začneme dělat, převést na její kanonický tvar.

Tato funkce je složená, vnější funkce (tj. operace, která se dělá při výpočtu poslední), je exponenciála e^y (jejíž derivace je e^y). Použijeme řetízkové pravidlo, jako obvykle derivujeme nejprve to, co se při výpočtu dělá poslední.

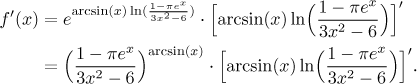
Protože budeme první člen (tu obecnou mocninu) kopírovat ve všech následujících krocích, nahradíme ji dočasně kosočtvercovou značkou. Výraz, který teď musíme derivovat, je součin dvou členů (tj. poslední operace je násobení), tedy použijeme součinové pravidlo.

Derivace vlevo je elementární, napravo potřebujeme derivovat složenou funkci pomocí řetízkového pravidla, vně (při výpočtu se dělá poslední) máme ln(y) s derivací 1/y, tím tedy začneme.

Teď je třeba použít podílové pravidlo.

Oba výrazy, které je třeba derivovat, jsou lineární kombinace jednoduchých členů, takže výpočet dokončíme.

Teď potřebujeme najít definiční obor. Začneme danou funkcí. Coby obecnou mocninu ji musíme zkoumat v jejím kanonickém tvaru "e na ln". Arcsinus vylučuje všechna x s |x| > 1, takže se rovnou omezíme na ⟨−1,1⟩. Další podmínka je, že zlomek v logaritmu musí být kladný. Pro x z rozmezí ⟨−1,1⟩ je jmenovatel záporný, takže potřebujeme, aby byl záporný i čitatel, což je pravda pro

x > ln(1/π) = −ln(π).

Všimněte si nicméně, že ln(π) > 1, takže tato podmínka je vlastně splněna pro všechna x z ⟨−1,1⟩. Proto

D( f ) = ⟨−1,1⟩.

Protože derivace můžeme dělat jen na otevřených množinách, ztrácíme koncové body, ale pro ostatní x z definičního oboru f už derivace existuje. Dostáváme tedy

D( f ′ ) = (−1,1).

Další příklad
Zpět na Řešené příklady - Derivace