Výpočet derivace: Přehled metod

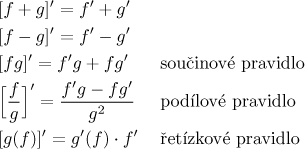
Pokud chcete nějaký text o derivaci sledovat zároveň ve vedlejším okně, klikněte sem pro Teorii a sem pro Řešené příklady.

Zde ukážeme algoritmus pro výpočet derivace. Derivování je základem pro většinu výpočtů v reálné analýze, takže byste se to měli dobře naučit. Potřebná úroveň znalosti je velice snadno popsatelná: Musíte si být jisti, že dokážete najít (bez většího přemýšlení) derivaci libovolné funkce, která vám příjde do cesty, pokud je poskládaná z elementárních funkcí a algebraických operací či skládání. Níže představený algoritmus právě toto dokáže.

Abyste uměli derivovat, je třeba znát nazpamět dvě základní věci:
Slovník neboli elementární derivace.
Gramatiku, což znamená pět základních pravidel pro operace:

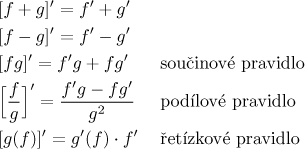
Také se hodí si pamatovat, že derivace je lineární, takže když derivujeme součty, stačí derivovat každý člen zvlášť; multiplikativní konstanty zase mohou být vytaženy před derivaci.

Jsou dvě možnosti derivování. Někdy se dají použít elementární derivace a rovnou napsat výsledek. Vzorce z elementárních derivací je ale možné použít jen tak, jak jsou uvedeny, jakákoliv modifikace znamená, že přestávají fungovat a je třeba použít pravidla. Takže zatímco můžeme psát například že derivace sin(x) je cos(x), toto pravidlo už nefunguje na modifikace jako sin(2x), sin(x²), sin²(x) atd. Například derivace sin(2x) rozhodně není cos(2x).

Druhá možnost je, že máme výraz, který není na seznamu elementárních derivací. Pak je třeba použít pravidla k tomu, aby se rozložil na své základní stavební jednotky, které jsou nakonec udělány pomocí elementárních derivací. Příslušný algoritmus je uveden níže, ale předtím ještě jednu poznámku o značení.

Začátečníci někdy mívají problémy s aplikací derivačního symbolu, například je může mást značení v řetízkovém pravidle výše. Je to ale jednoduché. Začneme příkladem. Uvažujme funkci f (x) = x². Když napíšeme f ′(5), pak symbol f ′ reprezentuje konkrétní funkci, jmenovitě funkci f ′(x) = 2x, do které dosazujeme 5:  f ′(5) = 10. Na druhou stranu značení [f (5)]′ znamená, že nejprve dosadíme 5 a teprve poté derivujeme. Protože je f (5) konstanta, dostaneme [f (5)]′ = [25]′ = 0. Pokud vám toto dává smysl, pak by měla být jasná i ta dvě značení z řetízkového pravidla. [g( f )]′ znamená, že nejprve vyhodnotíme skládání a pak derivujeme tu složenou funkci. Na druhou stranu g′( f ) znamená, že nejprve derivujeme g jako samostatnou funkci a pak dosadíme f do vzniklé derivace (tj. skládáme derivaci funkce g s vnitřní funkcí f ).

Derivace výrazu

Algoritmus pro derivaci.
Krok 1. Podíváme se na výraz, který se má derivovat, a identifikujeme operaci, která se dělá poslední. To může být algebraická operace nebo vnější funkce v kompozici. Pokud si tohle potřebujete připomenout, podívejte se na poznámku o pořadí výpočtu.
Krok 2. Podle toho, jaká je "poslední operace", použijte příslušné gramatické pravidlo. Pravidlo rozdělí derivovaný výraz na menší, některé z nich bude třeba derivovat.
Krok 3. Podívejte se na derivace, které zůstaly po pravidle v Kroku 2. Pokud jsou všechny elementární, použijte slovník. Derivace je hotova. Pokud jsou některé derivace složitější, pro každou z nich zopakujte postup počínaje Krokem 1.

Všimněte si, že žádné z výše uvedených pravidel nebo elementárních limit nefungují na obecné mocniny. Ty je třeba derivovat v jejich kanonickém tvaru f ^g = e^ln( f )g.
Není také žádné pravidlo pro derivaci absolutní hodnoty. Funkce, které ji obsahují, se musí přepsat na funkci danou rozpisem, viz níže.

Pozor! Výsledky, které získáme tímto algoritmem, dávají derivaci daného výrazu pouze v takových bodech, kdy výraz existuje na jejich okolí. To znamená, že pomocí tohoto algoritmu můžeme hledat derivaci funkce v bodech, kde je funkce definovaná jedním výrazem na okolí. Co se stane, když tohle neplatí, například když je f dána jedním vzorcem nalevo a jiným napravo od bodu, kde chceme derivaci? Správný postup je popsán níže.

Derivace jako intuitivní proces. Je více způsobů, kterým se pravidla dají pamatovat a aplikovat, já mám nejlepší výsledky s intuitivním přístupem "zderivuj a zapomeň". Derivování je trochu jako loupání cibule. Vždy vidíte jen tu vrchní slupku, tedy operaci, která se dělá poslední. Vše ostatní, ať už jakkoliv komplikované, je v té chvíli irelevantní až na to, že se účastní jako části v té vnější operaci. Nemusíme se o ně starat, protože jsou "schované" vnější vrstvou. Když aplikujete příslušné pravidlo na vnější operaci, tak je už tato konkrétní operace udělána a už se dál o ni nemusíte starat (kromě napsání věcí, které z ní vznikly), jakmile je jednou zderivovaná (aplikováním pravidla), můžete na ni zapomenout a přejít k další vrstvě; protože ta vnější je udělána, odhalila se nám ta další.

Nejlépe je to vidět na řetízkovém pravidle. Pokud například derivujeme cos(g(x)), pravidlo říká

[cos(g(x))]′ = −sin(g(x))⋅[g(x)]′.

Jak to souhlasí s tím, co jsme teď říkali? Vnější operací je kosinus a je nám teď jedno, co je uvnitř, kosinus to před námi schovává. Proto zderivujeme kosinus, řetízkové pravidlo říká, že do té derivace máme dosadit to, co v něm bylo, a pak udělat "krát". V tomto okamžiku už je kosinus hotov, zmizel z příkladu, konečně vidíme, co je v něm, a je čas to derivovat.

Podobně můžeme interpretovat třeba i součinové pravidlo. Když chceme derivovat f ⋅g, tak je nám v té chvíli úplně jedno, co jsou ty jednotlivé faktory, my se soustředíme jen na vnější operaci. Pravidlo říká, že abychom zderivovali tuto operaci, máme přejít k výrazu f ′⋅g + f ⋅g′. Součin je tak z příkladu pryč, zmizel z derivace, přejdeme na další úroveň a podíváme se na faktory f a g, které nám předtím byly skryty. Tato odlupovací finta se opakuje, dokud nedojdeme k elementárním derivacím.

Jak už jsme řekli, toto je jen jeden z možných přístupů k derivaci. Někteří lidé to raději vidí jinak, například přísně formálně (při každém kroku si poznamenají, které části jsou f a které g a používají pravidla doslovně). Dělejte to, jak se vám dělá nejlépe.

Příklad: Najdi derivaci

Řešení: Poslední provedená operace je násobení, daná funkce je součinem uzávorkované části a zlomku. Proto aplikujeme součinové pravidlo.

Dostali jsme dva členy s derivací, žádný z nich není elementární funkce. Proto budeme každý z nich brát jako nový příklad.

První výraz v závorce má jako poslední operaci sčítání. Není jasné, které z těch dvou sčítání se dělá poslední, ale nám je to jedno, protože linearita říká, že máme prostě derivovat každý člen zvlášť.

Druhý derivovaný člen je jasný zlomek, takže podílové pravidlo.

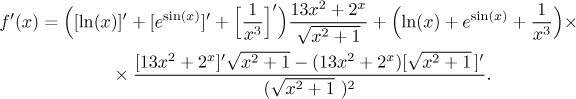
Teď máme spoustu derivací, vezmeme to odleva. Logaritmus je elementární funkce, jehož derivace je ve slovníku. Druhý člen je komplikovanější. Poslední operace tam je exponenciála, takže to je složená funkce a je třeba použít řetízkové pravidlo, například ve tvaru [e ^y]′ = e ^yy′. Další člen také vypadá trochu komplikovaněji, jmenovitě jako zlomek, a podílové pravidlo by opravdu fungovalo. Zkušený derivátor ale ví, že takové výrazy je lepší derivovat změněné v mocninu.

Tak dál k poslednímu zlomku. První člen nahoře je lineární kombinace, takže použijeme linearitu derivace. Jinými slovy, víme, že máme zderivovat každý sčítanec zvlášť, u prvního dokonce můžeme vytáhnout násobící konstantu ven z derivace. Druhý derivovaný člen (ten na konci) je složená funkce, jako poslední děláme druhou odmocninu, takže použijeme řetízkové pravidlo.

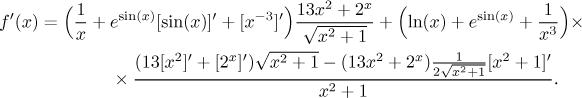
A jsme skoro tam, zase to vezmeme odleva. Derivace sinu a x⁻³ jsou ve slovníku. V posledním zlomku zase máme elementární derivace x² a 2^x. Poslední derivace je součet, takže derivujeme každý člen zvlášť.

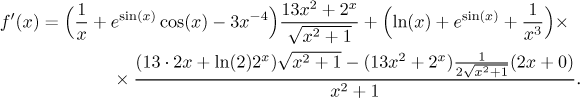
Zbývá to trochu učesat a podívat se po definičním oboru. Přepíšeme zápornou mocninu jako zlomek, vypadá to tak lépe. No a ten velký zlomek se podstatně zjednoduší, pokud vytáhneme z čitatele tu odmocninu z jeho druhého členu.

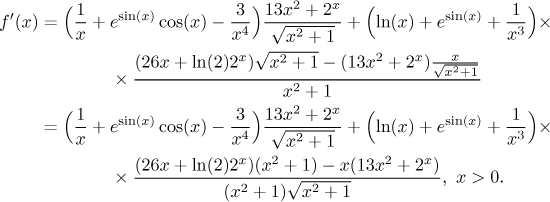
Všimněte si, že definiční obor je jen x > 0, ačkoliv výraz samotný je definován i pro záporná x. Definiční obor derivace je ale omezen především definičním oborem dané funkce.

Poznámky:
1. Pokud nepřepíšeme 1/x³ jako zápornou mocninu, ale použijeme podílové pravidlo, dostaneme stejnou odpověď, jen to trvá déle.

2. Co se stane, když zapomeneme, že se multiplikativní konstanty dají vytáhnout z derivace? Namísto jednoduchého výpočtu [13x²]′ = 13[x²]′ použijeme součinové pravidlo a dostaneme totéž:

3. Zkušený derivovač by nepsal všechny kroky. Když se na daný výraz aplikují jednotlivá pravidla, tak výraz "rozkvétá" či se "rozvětvuje", s každým krokem je více komplikovaný. Je v tom ale logika, a pokud máte zkušenosti, udržíte toho docela dost v hlavě. Často se tak dá psát rovnou odpověď, kterou vytváříme kousek po kousku. Pokud je daný výraz složitější, tak to může být nebezpečné, protože je snadné při derivování jedné části zapomenout, že ještě musíme zderivovat jinou, taky se občas poplete závorkování. Dobrá ochrana je volit zlatou střední cestu. Udělejte v hlavě, kolik se tam vleze, a zjednodušujte si celkový obrázek tím, že si nějaké části necháte "na potom" pomocí značení []′. Například ten příklad mohl být udělán ve dvou krocích takto:

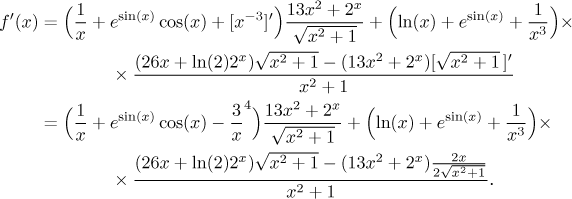
Otázka: Najděte f ′₊(a).

Nejlepší případ: Jestliže je funkce f dána konkrétním výrazem na nějakém okolí a, pak najdeme (oboustrannou) derivaci pomocí algoritmu nahoře a jednostranná derivace musí být stejná.

Typický případ: Funkce f je dána konkrétným výrazem na nějakém pravém okolí ⟨a,a + b) bodu a a onen výraz je tam spojitý. Pak můžeme použít báječnou větu:

jinými slovy najdeme derivaci daného výrazu pomocí základního algoritmu pro x > a a pak uděláme limitu této derivace pro x→a⁺. Pro příklad se podívejte na sekci Derivace a limita v části Teorie - Věta o střední hodnotě.

Jiné případy: Pokazit se toho může docela dost, je nemožné pokrýt všechny možné případy. V obecném případě, pokud nefungují výše popsané triky, tak obvykle jdeme zpět k definici a zkusíme to spočítat.

Otázka: Najděte f ′_-(a).

Je jasné, že použijeme příslušné modifikace předchozího postupu.

Funkce dané rozpisem jsou funkce, které jsou definovány různými výrazy na různých množinách (viz Úvod v části Funkce - Teorie - Reálné funkce). Budeme teď ignorovat příšery a soustředíme se na rozumné funkce rozpisem, ty, jejichž definice je založena na intervalech, které jdou jeden za druhým a je jich konečně mnoho (některé intervaly mohou být degenerované, tj. jeden bod).

Postup: Uvažujme "rozumnou" funkci f definovanou rozpisem.
Krok 1. Pro každý nedegenerovaný interval v definici f najdeme derivaci příslušného výrazu, který tam dává funkci. Tento výsledek pak také dává derivaci funkce f na vnitřku tohoto intervalu.
Krok 2. Jestliže je definiční obor f pokryt vnitřky intervalů z Kroku 1, pak jsme hotovi. Jinak existují body v definičním oboru f, které nejsou těmi vnitřky pokryty, a my se potřebujeme podívat, jak je to tam s f ′. Uvažujme jeden takový bod a.
a) Jestliže je to koncový bod intervalu z definice a také koncový bod definičního oboru, pak je f definovaná na nějakém levém nebo pravém okolí a, ale ne na druhé straně. Proto tam není žádná derivace, ale může tam být derivace jednostranná. Toto prozkoumáme způsobem popsaným výše. Připomeňme, že pokud není f v bodě a spojitá zprava/zleva, pak tam nemůže mít příslušnou jednostrannou derivaci, takže nemusíme ztrácet čas jejím hledáním.

b) Druhý zajímavý případ je, když je a vnitřní bod definičního oboru, ale ne nějakého intervalu z definice f. Pak je f nejspíše definovaná rozdílnými vzorci nalevo a napravo od a. To znamená, že ačkoliv je zde šance na normální oboustrannou derivaci, nedostaneme ji pomocí standardního algoritmu (viz odstavec Pozor! pod algoritmem). Zase, pokud funkce není spojitá v a, pak rovnou víme, že tam derivace není.

Předpokládejme proto, že je f spojitá v a a definovaná dvěma různými výrazy nalevo a napravo od a. Pak můžeme najít jednostranné derivace pomocí toho limitního triku popsaného výše a porovnat je. Pokud souhlasí, pak také dají derivaci f v a.

Příklad: Najděte derivaci absolutní hodnoty f (x) = |x|.

Protože pro absolutní hodnotu není pravidlo, začneme tím, že se jí zbavíme:

Protože je f definovaná výrazem x na otevřeném intervalu (0,∞), najdeme tam f ′ aplikací obvyklého algoritmu na výrazx. Podobně najdeme f ′ na (−∞,0) aplikací obvyklého algoritmu na výraz -x. Máme tedy

Zbývá najít derivaci v 0. Absolutní hodnota je tam spojitá, máme pěkné výrazy nalevo a napravo, takže použijeme limitní trik:

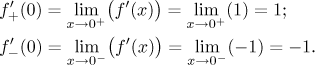
Odpověď je tedy

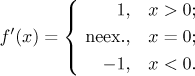
Pro další příklady derivací viz Řešené příklady - Derivace, ale derivování je samozřejmě i v Řešených příkladech na ostatní témata v části Derivace.