Příklad: Najděte derivaci funkce

Řešení: Derivaci nemůžeme najít přímo kvůli těm absolutním hodnotám, tak se jich nejprve musíme zbavit tak, že rozebereme znaménka výrazů uvnitř těchto absolutních hodnot. Dělící body jsou x = 0 a x = π. Dostaneme

(Trochu netradičně jsme dali rovnítka všude, abychom čtenáři připomněli, že je úplně jedno, kam je dáme, a každý si může vybrat. Pro body zlomu totiž obě varianty musí dát stejný výsledek.) Toto je funkce definovaná po částech. Derivaci můžeme hledat pomocí pravidel na vnitřku intervalů z jejího popisu. Nejprve podrobně ukážeme, jak se najde derivace pro x < 0. Tam derivujeme pomocí pravidel příslušný výraz.

Díky linearitě můžeme derivovat zvlášť každou část. První je kosinus (jehož derivace je mínus sinus) složený s vnitřní funkcí, takže použijeme řetízkové pravidlo a nejprve derivujeme kosinus (počítá se poslední, tedy derivuje první). Druhá část je také složení, takže použijeme řetízkové pravidlo s vnější funkcí e^y, jejíž derivace je e^y (zase: při výpočtu se dělá poslední, tudíž s ní začneme při derivování). Dostaneme

Výraz v první derivaci je zase složená funkce, poslední oeprace (vnější funkce) je y⁵, takže použijeme řetízkové pravidlo s [y⁵]′ = 5y⁴. Druhý derivovaný výraz je lineární výraz, jehož derivace je elementární.

Konečně se dostáváme k výsledku, zbývající derivace je aplikovaná na lineární výraz.

Podobně derivujeme výrazy, které definují f na zbývajících dvou otevřených intervalech, dostaneme tak (zkuste to)

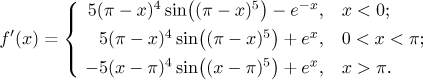
Zbývá zjistit, co se děje s derivací v dělících bodech. Na to použijeme jednostranné derivace a užitečnou větu (ze sekce Teorie - Věta o střední hodnotě - Derivace a limita), která nám umožňuje hledat tyto jednostranné derivace pomocí limity derivací, které už jsme spočítali. Jeden z předpokladů této věty je spojitost ve zkoumaném bodě, ale to tady platí, protože původně jsme měli jeden výraz s absolutními hodnotami, který je spojitý všude.

Nejprve se podíváme na počátek.

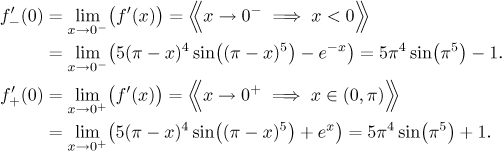
Protože se tyto dvě jednostranné derivace nerovnají, není v x = 0 derivace.

Teď se podíváme na pí.

Protože se tyto dvě jednostranné derivace rovnají, dostáváme derivaci v π. Všimneme si, že oba výrazy, které jsme použili v limitě, lze použít také v bodě π, takže nemusíme derivaci v π uvádět jako speciální případ, ale můžeme ji zahrnout do jednoho i třeba obou příslušných intervalů (vyjde to nastejno). Dostáváme

Další příklad
Zpět na Řešené příklady - Derivace