Příklad: Najděte derivaci funkce

Řešení: Funkce je dána vzorečkem, takže budeme derivovat pomocí pravidel. Je tu jedna mírně netypická věc, ve vzorci vidíme dva parametry p a q, jejichž hodnoty neznáme. To ale ve skutečnosti není problém. Když máme parametry, tak se rozumí, že reprezentují dvě pevně zvolená čísla, a ačkoliv nevíme jaká, tak víme, že se nemění. V našem derivačním postupu tedy budou hrát stejnou roli, jako jiné konstanty ve vzorci (třeba číslo 13).

Jinými slovy, stačí si na místě p a q představit nějaká konkrétní čísla a rozmyslet si, co bychom v takové situaci dělali, a pak to uděláme s písmeny namísto čísel. Jdeme na to.

Poslední operace při výpočtu je logaritmus, takže tu máme složený výraz s logaritmem coby vnější funkcí, která se derivuje nejdřív (pomocí řetízkového pravidla). Připomeneme si, že derivace ln(y) je 1/y.

Teď je poslední operací násobení, takže aplikujeme součinové pravidlo.

V prvním členu se derivuje obyčejná mocnina, druhá derivace je zase složená funkce, tentokráte velice snadná a řetízkové pravidlo říká, co máme dělat, nejprve derivujeme hyperbolický kosinus.

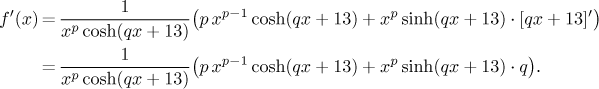
Jaký je definiční obor této derivace? Začneme definičním oborem dané funkce. Logaritmus chce mít kladný argument. Co víme o výrazu uvnitř? Hyperbolický kosinus akceptuje cokoliv, takže tam omezení není, a jeho hodnoty jsou vždy nejméně 1. mocnina je vybíravější. Protože nevíme, jakou hodnotu má parametr p, musíme se podívat na nejhorší možný případ, když je to jen nějaké reálné číslo, a pak požadujeme podmínku x > 0. Vidíme také, že za tohoto omezení je celý výraz v logartimu kladný, takže i tato podmínka je splněna. Nakonec se podíváme, že také výsledek (ta derivace) existuje kdykoliv je x kladné, takže jde o hledanou podmínku platnosti našeho výpočtu.

Další příklad
Zpět na Řešené příklady - Derivace