Příklad: Najděte derivaci funkce

Řešení: Funkce je dána vzorečkem, takže budeme derivovat pomocí pravidel. Poslední operace při výpočtu je arcsin, takže tu máme složený výraz s arcsinem coby vnější funkcí, která se derivuje nejdřív (pomocí řetízkového pravidla).

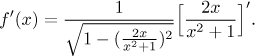
Teď je poslední operací dělení, takže aplikujeme podílové pravidlo.

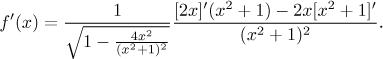
Teď použijeme linearitu a elementární derivace a dokončíme výpočet.

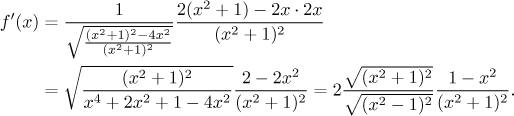
Jaký je definiční obor této derivace? Začneme definičním oborem dané funkce. Protože x² + 1 > 0, nemusíme mít starosti ohledně toho zlomku. Jediné omezení tedy pochází z arcsinu, který vyžaduje, aby ten zlomek byl mezi −1 a 1 včetně. Zkusíme vyřešit obě rovnice.

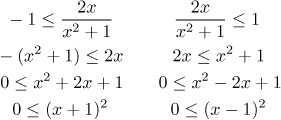
Vidíme, že rovnice platí pro všechna reálná čísla x, proto

D( f ) = ℝ.

Je u derivace něco jinak? V prvním zlomku je podmínka, která vylučuje případ x² = 1, takže tento vzorec nedává derivaci pro x rovno −1 a 1. To ale ještě neznamená, že by tam ta derivace nemohla být, jen to říká, že přístup přes pravidla nepomůže. Zkusíme se tedy na derivaci v těchto bodech podívat jako na samostatný problém, půjdeme na to přes jednostranné derivace. Protože je daná funkce f všude spojitá, můžeme jednostranné derivace najít pomocí limity (viz příslušná věta v části Teorie - Věta o střední hodnotě - Derivace a limita).

Než ale začneme počítat, zkusíme zjednodušit vzorec, který jsme právě dostali. Víme, že odmocnina z něčeho na druhou není to něco, ale absolutní hodnota toho něčeho. Pomocí tohoto pravidla derivaci přepíšeme a pak se zbavíme absolutních hodnot.

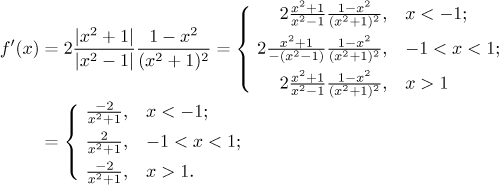
Teď už jsme připraveni počítat jednostranné derivace. Začneme v bodě x = −1:

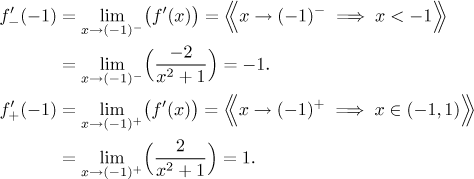
Protože jednostranné derivace nesouhlasí, není derivace v bodě x = −1. Stejný závěr platí o x = 1, protože tam máme

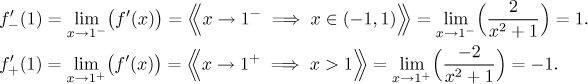
Máme tedy následující situaci: Daná funkce je definována na celé reálné ose, je definována zdánlivě nevinným výrazem bez absolutních hodnot, přesto má ale derivaci jen na menší množině:

D( f ′) = (−∞,−1)∪(−1,1)∪(1,∞).

I takové věci se někdy stanou.

Další příklad
Zpět na Řešené příklady - Derivace