Triky s Větou o střední hodnotě

Věta o sřední hodnotě se dá použít na docela zajímavé věci.

Porovnávání funkcí

Fakt.
Nechť f a g jsou funkce spojité na intervalu I a diferencovatelné na jeho vnitřku I ^o. Jestliže f ′ = g′ na I ^o, pak existuje konstanta C taková, že f (x) = g(x) + C na I.

Jestliže navíc existuje bod c v I takový, že f (c) = g(c), pak f = g na I.

Toto tvrzení získáme tak, že uvažujeme rozdíl g − f a aplikujeme příslušná tvrzení ze sekce Derivace a monotonie. Smysl je jasný. Jestliže mají dvě funkce stejné derivace, pak tečny v odpovídajících bodech musí mít stejné směrnice, jinak řečeno musí jít jejich grafy nahoru a dolů stejným způsobem. Když si představíte, že dvě tužky začnou v určité vzdálenosti nad sebou nalevo a pak se posunují doprava stejnou rychlostí a kopírují jedna po druhé stoupání a klesání, pak musíte dojít k jedinému závěru: Jeden graf by měl být jen posunutím druhého, v jistém smyslu jsou paralelní.

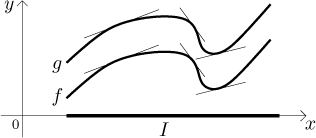
Pokud ty dva grafy také sdílí nějaký bod a jsou paralelní, pak musí být stejné. To se používá k důkazu, že se dva výrazy rovnají, když to neumíme udělat algebraicky.

Příklad: Dokažte, že pro x > 0 platí

Řešení: Nezdá se, že by existoval nějaký zjevný algebraický postup, zkusíme tedy ten Fakt. Definujeme f (x) = arctg(x) a g(x) = π/2-arctg(1/x), uvažujme interval I = (0,∞). Nejprve se podíváme na derivace těch dvou funkcí:

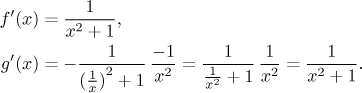
Jsou tedy paralelní. Teď potřebujeme dosadit nějaký bod, abychom ukázali, že se rovnají. Zkusíme x = 1.

Podle Faktu jsou si tedy ony dvě funkce rovny.

Poznamenejme, že někdy není úplně snadné najít vhodný bod k dosazení. Pak se dá použít trik a porovnat limity, například v koncových bodech. Zde se dá porovnávat takto:

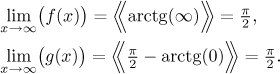
Podobně dokazujeme nerovnosti, ale tam je třeba být trochu opatrnější.

Fakt.
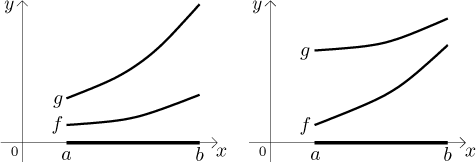
Nechť f a g jsou funkce spojité na intervalu I = ⟨a,b) nebo I = ⟨a,b⟩ a diferencovatelné na jeho vnitřku (a,b). Jestliže f ′ ≤ g′ na (a,b) a f (a) ≤ g(a), pak f  ≤ g na I.

Nechť f a g jsou funkce spojité na intervalu I = (a,b⟩ nebo I = ⟨a,b⟩ a diferencovatelné na jeho vnitřku (a,b). Jestliže f ′ ≥ g′ na (a,b) a f (b) ≤ g(b), pak f  ≤ g na I.

Zde jsou typické situace pro obě verze:

Docela často se tato tvrzení používají s jednou funkcí rovnou identicky nule neboli k důkazu, že daná funkce například není záporná:

Nechť f je funkce spojitá na intervalu I = ⟨a,b) nebo I = ⟨a,b⟩ a diferencovatelné na jeho vnitřku (a,b). Jestliže f ′ ≥ 0 na (a,b) a f (a) ≥ 0, pak f  ≥ 0 na I.

Všechna tato porovnávací tvrzení mají také "ostrou" verzi, ukážeme si to třeba u posledního:

Nechť f je funkce spojitá na intervalu I = ⟨a,b) nebo I = ⟨a,b⟩ a diferencovatelné na jeho vnitřku (a,b). Jestliže f ′ ≥ 0 na (a,b) a f (a) > 0, pak f > 0 na I.

Předpokládejme, že máme pěknou (spojitou) funkci na intervalu I. Předpokládejme dále, že má v tomto intervalu dva nulové body. Pak musí mít logicky mezi těmito dvěma body kopeček nebo dolík, a jestliže máme diferencovatelnost, pak Rolleova věta tvrdí, že mezi těmi dvěma kořeny je nějaký bod, kde je derivace nulová. Pokud máme kořenů více, můžeme se podívat na všechny jejich následující páry a pro každý najdeme místo s nulovou derivací.

Fakt.
Nechť f je funkce spojitá na intervalu I a diferencovatelná na jeho vnitřku I ^o. Jestliže f má k různých nulových bodů v I, pak její derivace f ′ musí mít nejméně k−1 různých nulových bodů v I.

Jestliže je tato derivace diferencovatelná, můžeme zkusit další krok. Indukcí dostaneme

Důsledek.
Nechť f je funkce, která má n−1 spojitých derivací na intervalu I a n-tou derivaci na jeho vnitřku I ^o. Jestliže f má k různých nulových bodů v I (kde k > n), pak její n-tá derivace f ⁽ⁿ⁾ musí mít nejméně k-n různých nulových bodů v I.

Tento fakt se někdy používá k důkazu, že nějaká funkce nemá mnoho kořenů. Předpokládáme sporem, že má, pak se podíváme na její derivaci a doufáme, že nastane průšvih.

Příklad: Dokažte, že kubický polynom f (x) = x³ + x má nanejvýš jeden kořen.

Sporem, předpokládejme, že má kořeny dva či více. Vezměme libovolné dva z nich, pak by podle Faktu měla mít derivace alespoň jeden nulový bod. To ale není možné, protože f ′(x) = 3x² + 1 > 0. Předpoklad dvou a více kořenů byl tedy špatný a je to hotovo.

Je také možné zkusit přímý postup, protože ten Důsledek lze také ekvivalentně napsat jako

Důsledek.
Nechť f je funkce, která má n−1 spojitých derivací na intervalu I a n-tou derivaci na jeho vnitřku I ^o. Jestliže n-tá derivace f ⁽ⁿ⁾ má k různých nulových bodů v I, pak f může mít nejvíše k+n různých nulových bodů v I.

Poznamenejme, že aby byl tento trik úspěšný, je třeba trochu štěstí. Spolehlivější metoda spočtení kořenů je určit monotonii dané funkce, což je obvykle snadné, když už máme její derivaci (viz Monotonie v části Teorie - Průběh funkce), a pak už i jen symbolický náčrt jasně ukáže, kolik je kořenů.

Zpět na Teorie - Věta o střední hodnotě