Věta o střední hodnotě a příbuzná tvrzení

Zde představíme tři základní věty diferenciálního počtu.

Věta (Rolleova věta).
Nechť a < b jsou reálná čísla. Nechť f je funkce spojitá na intervalu ⟨a,b⟩ a diferencovatelná na (a,b).
Jestliže f (a) = f (b), pak existuje c z (a,b) takové, že

Jaký je smysl tohoto tvrzení? Pokud jsou oba konce grafu na stejné úrovni, pak musí existovat bod, kde je tečna vodorovná:

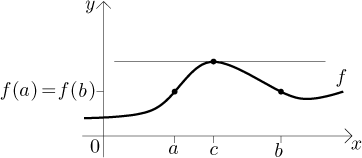
To zní jako něco, co by mělo být pravda. Abychom této větě lépe rozuměli, podíváme se na význam jednotlivých předpokladů. Je jich tam několik. Některé jsou o funkci: Má být spojitá, má mít derivaci, její konce mají být na stejné úrovni. Následující obrázek ukazuje, že porušení jediného z těchto předpokladů už udělá závěr neplatným, pro ony tři příklady nejsme schopni najít vodorovnou tečnu.

Máme také předpoklady o možině. Uzavřený interval je vlastně omezená, uzavřená a souvislá množina. Dvě z těchto podmínek jsou tak zásadní, že je nemůžeme vynechat, aniž by se věta nestala nesmyslnou. Pokud množina není omezená, nemá oba konce konečné, nelze tedy porovnávat, na jakých úrovních jsou konce grafu. Podobně ztrácíme koncové body pro otevřené množiny. Jediný zajímavý předpoklad o množině je tedy souvislost. Následující obrázek ukazuje, že když jej porušíme, pak už se nemůžeme spoléhat na existenci vodorovné tečny. Všimněte si, že funkce na obrázku je spojitá na označené omezené a uzavřené množině M a diferencovatelná na jejím vnitřku, oba konce jsou evidentně na stejné úrovni.

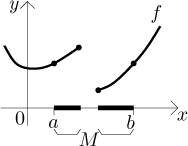
Obrázky tak ukazují, že pokud vynecháme byť jen jediný z předpokladů věty, tak už se na existenci vodorovné tečny nemůžeme spolehnout. Samozřejmě vodorovné tečny se mohou objevit u funkcí i bez těchto předpokladů, například na tomto obrázku funkce nesplňuje snad žádný a vodorovnou tečnu má:

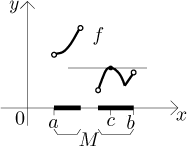
ale to už je jen otázkou štěstí, zatímco nás zajímá, kdy ji máme zaručenou. Poznamenejme ještě, že z diferencovatelnosti f na (a,b) už automaticky vyplývá, že je tam dotyčná funkce spojitá. Ten druhý předpoklad (o spojitosti) tedy v zásadě přináší jen dvě nové věci, a to je jednostranná spojitost v koncových bodech. Tam už to z derivace nevyplývá.

Pokud vezmeme obrázek, který vysvětloval Rolleovu větu, a nakloníme jej, tak to vypadá, že by všechno mělo pořád fungovat. A taky že ano, je jen otázkou, jak to pořádně zapsat.

Jaký má tato věta smysl? Pokud spojíme konce grafu f přímkou, pak je její směrnice přesně ten zlomek napravo. Věta říká, že musí existovat bod, kde má tečna stejnou směrnici. Jinými slovy, když spojíme konce grafu přímkou, pak musí existovat tečna, která je rovnoběžná s touto spojnicí.

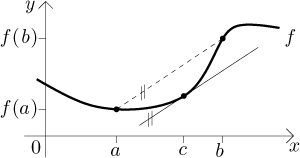
Tato věta je založena na Rolleově větě, takže bychom zde mohli zopakovat stejnou analýzu předpokladů, abychom ukázali, že jsou všechny nutné. Jinak řečeno, Rolleova věta je jen speciální případ Věty o střední hodnotě, takže pokud vynecháme předpoklad a Rolleova věta už neplatí, pak to také nefunguje ve Větě o střední hodnotě.

Tato věta má zajímavo interpretaci. Předpokládejme, že f je záznam dráhy (viz např. zde nebo tato poznámka). Pak je ten zlomek napravo vlastně průměrná rychlost, zatímco výraz nalevo je okamžitá rychlost v určitém čase. To říká, že když se pohybujeme rozumným způsobem (dostatečně hladce na to, aby byla derivace), pak jsme v některém okamžiku museli jet stejnou rychlostí, jako je průměrná rychlost.

Tuto sekci uzavřeme zobecněním Věty o střední hodnotě.

Tak tuhle větu je opravdu těžké vysvětlit, protože se nedá rozumně ukázat na obrázku. Jeden možný přístup k této větě je následující: Větu o střední hodnotě jsme dostali z Rolleovy tak, že jsme vzali obrázek od Rollea a naklonili jej. Abychom se dostali od Věty o střední hodnotě k Cauchymu, vezmeme proměnnou x a transformujeme ji v novou proměnnou vzorcem g(x). Pokud je tato transformace jednoduchá (například pokud graf zmáčkneme či posuneme nalevo/napravo), pak vypadá rozumně, že by závěr o rovnoběžných přímkách mohl stále platit. Tato věta ale také povoluje komplikovanější tranformace.

Všimněte si, že když vezmeme Cauchyho větu a použijeme ji s funkcí g(x) = x, dostaneme Větu o střední hodnotě. Cauchyho věta je tedy z těch tří nejsilnější, ale je tak abstraktní, že se velmi zřídka používá v konkrétních situacích. Z praktického pohledu je Věta o střední hodnotě králem. Bez Cauchyho věty bychom ale neměli l'Hospitalovo pravidlo z následující sekce, a představte si, že byste měli řešit limity bez l'H. Myslím, že lepší dobrozdání než tohle už Cauchyho věta nepotřebuje.

Derivace a limita
Zpět na Teorie - Věta o střední hodnotě