Náčrt parametrických funkcí: Přehled metod

Uvažujme parametrickou křivku danou rovnicemi
x = x(t),
y = y(t)   pro t z nějakého intervalu I.
Předpokládejme, že funkce x(t), y(t) jsou dvakrát diferencovatelné na I. Chceme tuto křivku nakreslit.

Algoritmus:
Krok 1. Zjistíme, co se děje "na koncích" I. Pokud je koncový bod I zahrnut do I, pak tento čas dosadíme do x a y, abychom zjistili, kde křivka začíná či končí. Pokud některý koncový bod zahrnut není, pak najdeme příslušnou jednostrannou limitu x a y vzhledem k t a pak tuto informaci interpretujeme.
Případ "obě limity vlastní": křivka jde do bodu daného limitami.
Případ "obě limity nevlastní": křivka jde do rohů podle znamének nekonečen v limitách, například jestli x→−∞ a y→∞, pak jde křivka do levého horního rohu. Asymptota se najde pomocí limit A = lim( y/x), B = lim( y − Ax), konvergují-li.
Případ "x→L, limita y nevlastní": křivka má svislou asymptotu v x = L a tulí se k této přímce u jejího horního či dolního konce podle znaménka nekonečna coby limity y.
Případ "limita x nevlastní, y→L": křivka má vodorovnou asymptotu y = L a tulí se k této přímce na pravém či levém konci podle znaménka nekonečna coby limity x.
Krok 2. Najdeme průsečíky s osami. Průsečíky s osou x jsou dány časy t splňujícími y(t) = 0, průsečíky s osou y jsou dány časy t splňujícími x(t) = 0. Dosazením těchto časů do x a y získáme prostorové souřadnice průsečíků.
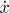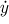Krok 3. Najdeme a , pak najdeme t z vnitřku I splňující 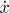 = 0 nebo 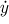 = 0. Toto jsou kritické časy. Dosadíme je do x a y, abychom zjistili, kde se křivka otáčí.
Zaznačíme data z Kroků 1, 2 a 3 v rovině. Je dobré si k nim poznamenat časy, ve kterých se tam křivka dostane.
Kritické časy rozdělí I na podintervaly. Pro každý z nich určíme znaménk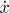a a 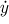, pak určíme znaménka prostorové derivace

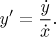
To se nejlépe dělá pomocí tabulky. Pro každý podinterval I, který dostáváme, nám časy z tohoto podintervalu dávají určitý úsek křivky a růst či klesání této části jako grafu je dáno příslušným znaménkem. Teď můžeme spojit body v obrázku dočasnými čarami, které těmto trendům vyhovují.
Krok 4. Najdeme druhé derivace funkcí x vzhledem k času a y a spočítáme druhou prostorovou derivaci

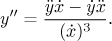
Najdeme časy t z vnitřku I, kdy je čitatel či jmenovatel této derivace nulový. Dosadíme tyto časy do x a y a najdeme body, kde křivka může měnit konvexitu. Tyto body zaznamenáme do obrázku.
Tyto časy rozdělí I na podintervaly. Pro každý z těchto časů určíme znaménko druhé prostorové derivace y′′, to se dělá nejlépe pomocí tabulky. Pro každý podinterval I, který dostáváme, určují časy z tohoto podintervalu úsek křivky, jehož konvexita je dána příslušným znaménkem y′′. Opravíme dočasné čáry, aby souhlasily s těmito daty.

Toto jsou hlavní kroky. Pokud má křivka konec v nějakém krajním bodě I (tj. pokud je tento bod zahrnut do I nebo tam dostáváme obě limity vlastní v Kroku 1), pak je také dobrý nápad určit příslušnou jednostrannou prostorovou derivaci v tomto bodě, ta nám řekne, kterým směrem má křivka vyrazit. Pokud je to například levý koncový bod t = a intervalu I a označíme x₀ = x(a), pak

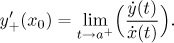
Pro více informací a další příklad viz Náčrt parametrických funkcí v části Teorie - Implicitní a parametrické funkce.

Příklad: Prozkoumejte parametrickou křivku
x = t⋅e^t,
y = t³ + 6t,   t ≥ −1.

Řešení: Interval I = ⟨−1,∞) obsahuje svůj levý koncový bod t = −1; dosazením do x a y dostaneme startovní bod pro křivku (−1/e,−7). Druhý koncový bod I je nekonečno, takže najdeme

Křivka tedy nakonec zmizí v pravém horním rohu. Limita y/x je v nekonečnu nula, což naznačuje vodorovnou asymptotu, ale limita pro B diverguje a proto asymptota není, jen funkce roste pomaleji a pomaleji (je táhnuta víc "doprava" než "nahoru"); očekáváme, že na tomto konci bude konkávní.

Průsečíky s osami: Průsečík s osou y je dán rovnicí x = t⋅e^t = 0, což má jen jedno řešení, t = 0. Tento čas dává bod (0,0).
Průsečík s osou x je dán rovnicí y = t³ + 6t = 0, což zase dává t = 0 a bod (0,0).

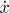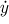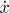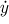Najdeme (t) = (t + 1)e^t, to je nula jen pro t = −1, což je koncový bod I, a tak se základní časový interval nerozdělí. Máme také (t) = 3t² + 6, zde není nulový bod. Graf daný touto křivkou má tedy stejnou monotonii pro všechny časy z I. Pro t > −1 jsou jak (t) tak (t) kladné, proto je také y′(x) kladné a graf roste.

Zbývá najít

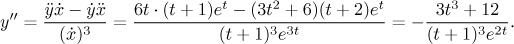
Tato derivace neexistuje pro t = −1 a zase tento bod budeme ignorovat, a je nulová, když t je třetí odmocnina z −4, což je méně než −1 tudíž ne uvnitř I, taky to tedy ignorujeme. Vidíme, že pro t > −1 je druhá prostorová derivace y′′(x) vždy záporná, proto je křivka jako graf konkávní.

Poslední údaj je jednostranná derivace na začátku křivky:

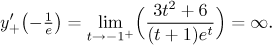
Křivka by tedy měla začít svisle nahoru. Protože po čase t = 0 už další časy nemáme, dodá lepší představu o grafu dosazení pár dalších časů, zkusíme t = 1 a dostaneme bod (e,7), pro čas t = 2 dostaneme bod (2e²,20). Jsme připraveni nakreslit obrázek.

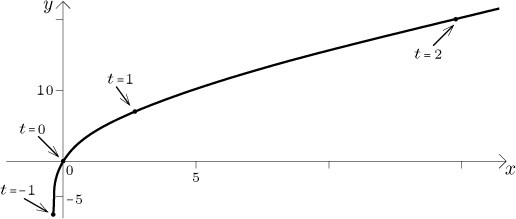
Pro další příklad viz Implicitní a parametrické funkce v části Řešené příklady.

Zpět na Přehled metod - Implicitní a parametrické funkce