Vlastnosti Riemannova integrálu

Začneme vlastnostmi, které by se měly zdát jasné díky tomu, že Riemannův integrál je vlastně obsah (matematický).

Fakt.
(i) Nechť f je Riemannovsky integrovatelná funkce na ⟨a,b⟩. Jestliže f ≥ 0 na ⟨a,b⟩, pak .
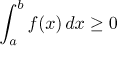Jestliže je f spojitá funkce na ⟨a,b⟩ a f > 0 na ⟨a,b⟩, pak .

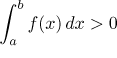(ii) Nechť f je Riemannovsky integrovatelná funkce na ⟨-a,a⟩. Jestliže je f lichá, pak .
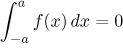Jestliže je f sudá, pak .

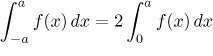(iii) Nechť f je Riemannovsky integrovatelná funkce na ⟨a,b⟩. Jestliže jsou m,M čísla splňující m ≤ f ≤ M na ⟨a,b⟩, pak

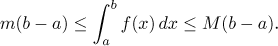
(iv) Nechť f a g jsou Riemannovsky integrovatelné funkce na ⟨a,b⟩. Jestliže f ≤ g na ⟨a,b⟩, pak

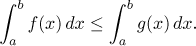
(v) Nechť f je Riemannovsky integrovatelná funkce na ⟨a,b⟩. Pak její absolutní hodnota | f | je také Riemannovsky integrovatelná funkce na ⟨a,b⟩ a

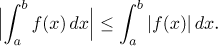
Obě vlastnosti v bodě (ii) plynou ze symetrie grafu již při pohledu na obrázek:

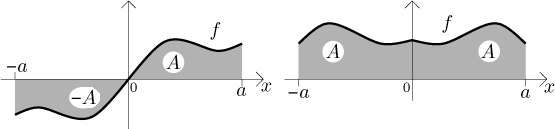
Jiné druhy symetrie mohou být také užitečné, například následující výsledek by neměl překvapit:

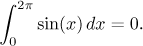
Opravdu, protože graf sinu je symetrický,

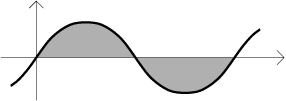
plochy nad a pod osou x se navzájem pokrátí.

Srovnávací vlastnosti v bodech (iii) a (iv) by také měly být zřejmé z obrázku:

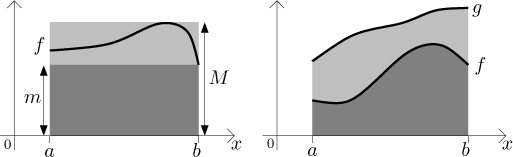
Zatímco výše zmíněná fakta jsou jen jednoduchá pozorování, následující vlastnosti jsou už docela důležité:

Věta.
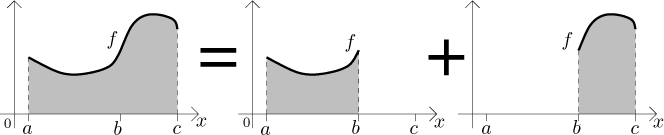
(i) Nechť a < b<c jsou reálná čísla, nechť f je funkce definovaná na intervalu ⟨a,c⟩. Funkce f je Riemannovsky integrovatelná na ⟨a,c⟩ tehdy a jen tehdy, pokud je Riemannovsky integrovatelná na obou intervalech ⟨a,b⟩ a ⟨b,c⟩; pak také

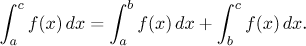
(ii) Nechť f je Riemannovsky integrovatelná funkce na ⟨a,b⟩, nechť k je reálné číslo. Pak funkce kf je Riemannovsky integrovatelná na ⟨a,b⟩ a

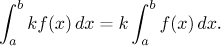
(iii) Nechť f a g jsou Riemannovsky integrovatelné funkce na ⟨a,b⟩. Pak je funkce f + g Riemannovsky integrovatelná na ⟨a,b⟩ a

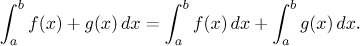
První vlastnost by měla být jasná z obrázku:

Druhá vlastnost plyne algebraicky z definice Riemannova integrálu. Konstanta k totiž může být vytknuta z infima a suprema f na jednotlivých podintervalech dělení, pak vytknuta ze sum v horních a dolních součtech a následně i z infima a suprema definujícího integrál.

Třetí vlastnost už není tak zjevná, protože supremum součtu dvou funkcí se rozhodně nerovná součtu suprem jednotlivých funkcí. Je zde ale k dispozici alespoň nerovnost, která vede správným směrem, a nakonec se to dá udolat. Existuje také geometrický argment, jehož nástin (spolu s pár zajímavostmi o obsahu) může zvědavý čtenář najít zde.

Newtonův integrál
Zpět na Teorie - Úvod do integrace
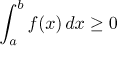
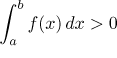
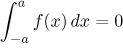
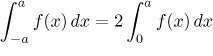