Newtonův integrál (primitivní funkce)

V této části uvedeme Newtonův integrál. Základní myšlenka je velice jednoduchá: derivace nám říká, jak se funkce mění v jiné funkce. Newtonův integrál se snaží tuto proceduru obrátit, k dané funkci se budeme snažit najít její "antiderivaci", což je název používaný v angličtině, česky se říká primitivní funkce.

Primitivní funkce

Definice.
Nechť f je funkce definovaná na intervalu I. Řekneme, že funkce F na I je primitivní funkcí k f na I, jestliže F je spojitá na I a F ′(x) = f (x) pro všechna x z vnitřku I ^O intervalu I.
Pokud taková primitivní funkce na I existuje, pak říkáme, že f je (Newtonovsky) integrovatelná na I.

Definice je dělána tímto způsobem hlavně proto, že pojmu primitivní funkce se používá převážně ve dvou situacích. Abychom měli derivaci funkce v jistém bodě x, musí být dotyčná funkce definovaná na určitém okolí tohoto bodu. Nejpřirozenější situace tedy je, když hledáme primitivní funkci k funkci f na otevřeném intervalu (a,b). Každý bod takového intervalu tam má okolí, takže hledaná primitivní funkce F má šanci být všude diferencovatelná a my požadujeme, aby F ′(x) = f (x) na (a,b). Protože diferencovatelnost implikuje spojitost (viz Derivace v části Derivace - Teorie - Úvod), taková F je pak automaticky i spojitá na (a,b) = (a,b)^O.

Často ovšem potřebujeme primitivní funkci F na uzavřeném intervalu ⟨a,b⟩. Definice pak říká, co přidat k předchozí přirozené situaci. Pořád ještě chceme, aby F ′ = f na (a,b), protože v koncových bodech derivaci mít nemůžeme (koncové body nemají okolí, kde by F určitě existovala). Abychom tedy popsali, co očekáváme od F v bodech a a b, použijeme tu druhou podmínku o spojitosti F na ⟨a,b⟩. Protože z předchozí poznámky víme, že diferencovatelnost F již implikuje spojitost na (a,b), tato druhá podmínka ve skutečnosti vlastně jen přidává požadavek na jednostrannou spojitost v koncových bodech našeho uzavřeného intervalu.

Příklad: Funkce F(x) = 3x − 1 je primitivní funkce k f (x) = 3 na intervalu (0,13⟩.
Tohle je jednoduché, F je zjevně spojitá na celé reálné ose, takže je také spojitá na (0,13⟩. Pro body z (0,13) = (0,13⟩^O také platí [3x−1]′ = 3, přesně jak je třeba.

Podobně ověříme, že také G(x) = 3x + 7 je primitivní funkcí k f (x) = 3 na (0,13⟩. Po pravdě řečeno, tyto dvě funkce jsou primitivní funkce k 3 na libovolném intervalu, typicky bychom uvažovali otevřené nebo uzavřené intervaly. Ten polouzavřený v příkladě byl spíš výjimkou, abychom ukázali, že to také jde.

Z příkladu vyplyne několik zajímavých věcí. Za prvé, jak jsme dostali ty primitivní funkce? Uhádli jsme je pomocí našich zkušeností s derivacemi. Na rozdíl od derivování, pro které jsme měli spolehlivý algoritmus a dokázali jsme zderivovat libovolnou funkci, kterou nám někdo napsal, primitivní funkce fungují podstatně jinak. K tomu se ještě dostaneme.

Druhá zajímavá věc je, že jsme k dané funkci získali více primitivních funkcí. Podle našich zkušeností s derivováním by nás dokonce nemělo překvapit, že pro libovolnou konstantu C je funkce 3x + C primitivní funkcí k f (x) = 3 na libovolném daném intervalu.

Jsou ještě jiné primitivní funkce k f (x) = 3? Nejsou. Následující věta říká, že přičtení konstanty k již známé primitivní funkci je jediný způsob, jak získat jiné primitivní funkce.

Věta.
Nechť F je primitivní funkce k f na nějakém intervalu I.
(i) Pro libovolnou konstantu C je funkce G(x) = F(x) + C rovněž primitivní funkcí k f na I.
(ii) Jestliže je H jiná primitivní funkce k f na I, pak existuje konstanta C taková, že H(x) = F(x) + C pro všechna x z I.

První část je snadná, protože G je spojitá všude, kde byla F, a

G′(x) = [F(x) + C]′ = F ′(x) + [C]′ = f (x) + 0 = f (x).

Je také možné se na situaci podívat z geometrického hlediska. Podmínka pro primitivní funkci F ′ = f znamená, že hledáme funkci, jejíž graf má tečny s dopředu předepsanými směrnicemi, jmenovitě směrnice tečny v bodě x je rovna f (x). Pokud takovou funkci F najdeme a pak k ní přičteme C, tak prostě jen posunujeme graf nahoru či dolů, takže směrnice tečen se nemění a posunutá funkce také splňuje potřebnou podmínku.

V opačném směru (ii) je dána funkce f, která předepisuje směrnice tečen dvou funkcí, F a H. Představte si, že se snažíme nakreslit jejich grafy. Začneme na jejich levých koncích a pak souběžně kreslíme. Protože v odpovídaících bodech mají tyto dva grafy stejné směrnice,rostou a klesají stejným způsobem; to znamená, že musíme oběma tužkami pohybovat stejným způsobem nahoru a dolů a kreslit paralelně.

Oba grafy tedy musí mít stejný tvar, jen posunutý nahoru či dolů.

Neexistuje značení, které by vyjádřilo fakt, že nějaké F je primitivní funkce k f. Máme ovšem značení pro množinu všech primitivních funkcí na daném intervalu. Tato množina se zapisuje takto . Říká se tomu Newtonův integrál funkce f na I.

Protože nám poslední věta říká přesně, jak množina primitivních funkcí vypadá, obvykle tuto množinu - Newtonův integrál - zapisujeme následujícím způsobem: Jestliže F je nějaká primitivní funkce k f na intervalu I, pak množinu všech primitivních funkcí k f na I zapisujeme

Proces nalezení primitivní funkce se nazývá integrování.

Všimněte si, že toto značení je ve skutečnosti špatně. Protože primitivní funkce tvoří množinu, správný zápis by měl být

Je to ale spousta psaní, a tak lidé dávají přednost tomu nesprávnému ale jednoduššímu zápisu. Pokud si budeme pamatovat, že ta věc na pravé straně je vlastně množina (nebo řečeno jinak, symbolizuje to libovolnou funkci daného tvaru, kde za C můžeme dát libovolnou konstantu), neměli bychom se dostat do průšvihu. Velice oblíbenou chybou je zapomenout na ono "+C". To je vážná chyba, která může u jednoduchých problémů vypadat formálně, ale u složitějších může vést k velkým problémům.

Příklad: První příklad může být také zapsán takto:

Pokud není interval nějak zadán, snažíme se při integraci pracovat na co největším intervalu, kde je to možné. Říká se tomu definiční obor integrálu. Získá se proniknutím definičního oboru integrované funkce s definičním oborem nalezené primitivní funkce, případně odejmutím bodů, kde tato primitivní funkce existuje, ale jsou nějaké problémy s derivací. U výše zmíněného příkladu bychom jako definiční obor dali celou množinu reálných čísel.

Protože definiční obor je ten největší interval, na kterém můžeme integrovat, daný výsledek lze také použít na libovolném "podintervalu". Z definice je zřejmé, že pokud je F primitivní funkcí k f na nějakém intervalu I a J je interval, který je podmnožinou I, pak F je také primitivní funkce k f na J.

Integrování jako "opak" derivování

To, že primitivních funkcí je mnoho, má další důsledek, který je třeba mít na paměti. Ačkoliv hledání primitivní funkce cítíme jako opak derivování, ve skutečnosti se touto procedurou derivace neruší. Víme například, že derivace funkce 3x + 7 je 3, když ale zkusíme najít k funkci 3 primitivní funkci, vybíráme nějakou funkci typu 3x + C a není nikde dáno, že musíme vybrat zrovna to 3x + 7, se kterým jsme začali. Takže obecně, pokud začneme s funkcí F, najdeme její derivaci f a pak zase najdeme primitivní funkci k f, nemusíme dostat nazpátek F. Nanejvýš můžeme říct, se ta nalezená primitivní funkce musí být vyjádřitelná jako F + D pro nějakou konstantu D.

Pokud použijeme značení Newtonova integrálu, pak otázka obracení derivace nemá ani smysl. Výsledkem integračního procesu není jedna funkce ale množina funkcí, takže se to prostě nemůže rovnat jedné funkci, se kterou jsme začali.

Pokud to zkusíme naopak, začneme funkcí f, najdeme nějakou její primitivní funkci F a pak ji zderivujeme, skončíme zase s f. Toto plyne přímo z definice. Ve značení Newtonova integrálu zase máme problém: Jak se derivuje množina funkcí? Pokud se ale na chvíli dohodneme, že tím myslíme, že zderivujeme všechny funkce dané množiny a uděláme z výsledků novou množinu, můžeme napsat (ne zcela přesně, ale vystihuje to podstatu):

Když jsme zaváděli integrální značení, začali jsme takto: "Jestliže je F nějaká primitivní funkce k f na I..." Jak takové F dostaneme? To je docela problém; jak dokonce uvidíme později, některé funkce ani primitivní funkci nemají, jinými slovy integrační proces selže! Než se k tomu ale dostaneme, podíváme se na některé vlastnosti primitivní funkce:

Věta (linearita integrálu).
(i) Nechť F je primitivní funkce k f na nějakém intervalu I. Pro každé reálné číslo k je (kF ) primitivní funkcí k (k f ) na I.
(ii) Nechť F je primitivní funkce k f na nějakém intervalu I, nechť G je primitivní funkce k g na I. Pak (F + G ) je primitivní funkce k ( f + g) na I.

Tato věta se vlastně velice lehce dokáže. Například funkce (kF ) je spojitá tam, kde byla i F, a z pravidel pro derivace se hned dostane [kF]′ = k[F]′ = kf. Druhé tvrzení je stejně zjevné.

Můžeme také vyjádřit tuto větu pomocí integrálního značení:

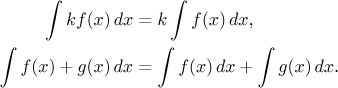
Když dojde na výpočty, je tento jazyk integrálů mnohem jednodušší k použití než primitivní funkce. Například díky zkušenosti z derivování lehce uhodneme i zapíšeme, že

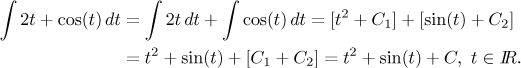
V příkladě jsme použili jinou proměnnou. Podobně jako u určitého integrálu, ani zde není konkrétní proměnná důležitá, záleží jen na vzorcích. Je třeba jen dát pozor, aby v průběhu výpočtu nedošlo omylem ke změně proměnné. Je dobré si zvyknout vždycky po skončení výpočtu zkontrolovat, že odpověď používá stejnou proměnnou jako otázka. Všimněte si také, že součet dvou libovolných konstant je nějaké číslo, zase libovolné. Proto když lidé integrují pomocí Věty o linearitě, nezatěžují se psaním více konstant a rovnou napíšou "+C".

Další dobrý zvyk je po výpočtu zkontrolovat, že jsme integrál našli správně. Toto je pěkná vlastnost integrace (možná jediná), že se dá lehce zkontrolovat správnost odpovědi tím, že ji zderivujeme a musí vyjít funkce z otázky:

Podobně zkontrojume správnost následujícího seznámku tabulkových integrálů, vycházejících z toho, co si pamatujeme o derivacích:

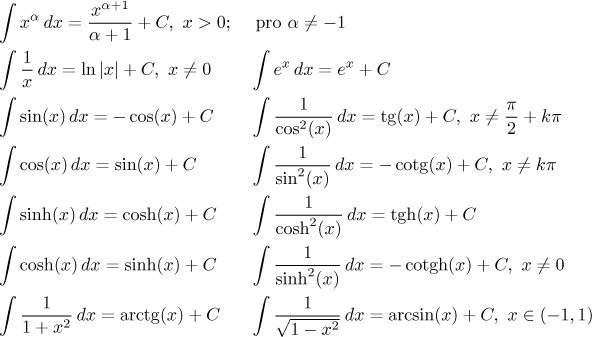
Definiční obory jsme zapisovali jen v případech, kdy se liší od celé reálné osy. Všimněte si, že u některých integrálů jsme definiční obor nezapsali správně. Důvodem je, že jsme definovali primitivní funkci na intervalu, takže nám není povoleno dát jako definiční obor komplikovanější množiny. V některých případech si ale můžeme vybrat mezi více intervaly.

Proto teď uvedeme důležitou konvenci. Když namísto intervalu specifikujeme u integrálu nějaké podmínky, pak tento integrál může být použit na libovolném intervalu, kerý vyhovuje těmto podmínkám. U prvního integrálu jsme vlastně ani neměli důvod se vyhnout správnému zápisu, ale psát x > 0 je jednodušší než vypisovat, že x náleží do (0,∞), a tak to tak lidi často píšou. Zde bychom měli poznamenat, že pro některé specifické hodnoty α je definiční obor větší, podle toho, kde je definována integrovaná mocnina. Pokud je mocnina rovna zápornému celému číslu (kromě −1, to je speciální případ), integrál může být použit na libovolném intervalu neobsahujícím 0. Pokud je α přirozené číslo, pak integrál platí na celé reálné ose.

Druhý integrál je dobrý příklad naší konvence. Primitivní funkci ln|x| lze použít například na (1,13) nebo ⟨−7,−2⟩. Největší možné intervaly jsou (0,∞) a (−∞,0).

Integrál vedoucí k tangensu je komplikovanější. Výsledek platí na inervalech neobsahujících specifikované body. Největší možné použitelné intervaly jsou tvaru .

Seznam tabulkových integrálů by mohl být samozřejmě delší. Každý derivační výsledek, který si pamatujete, se sem dá přidat v integrální formě. Nicméně ty výše vypsané jsou ty nejdůležitější, bez jejich zapamatování máte malou naději vyřešit dané integrály, ale na druhou stranu by také právě tyto měly stačit na většinu problémů. Samozřejmě, pokud si pamatujete víc, vaše šance na úspěch se zvýší.

Tohle je asi dobré místo připomenout, že když se integruje zlomek, lidi často píšou dx (nebo jiný diferenciál použitý v integrálu) do jmenovatele, aby zkrátili zápis. Například se dá psát

Teď se podíváme na několik problémů, na kterých si také ukážeme pár jednoduchých a populárních triků. První řešení zapíšeme velmi podrobně, zkušený integrátor by některé kroky vynechal.

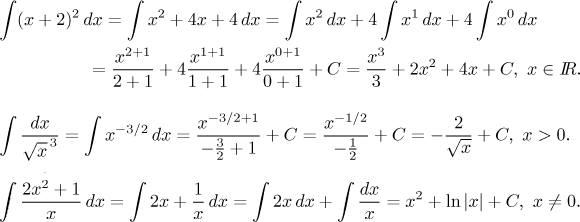
Udělejte si derivací zkoušku, že je to dobře.

Integrační postup, který jsme zrovna viděli, vám asi dost připomíná derivování. Pamatujeme si několik tabulkových integrálů, pamatujeme si pár pravidel a zbytek je algebra. Bohužel, toto je jedna z nevýhod integrace, možná ta hlavní. Ten dojem o algebraickém přístupu je správný, ale na rozdíl od derivování máme pouze dvě pravidla citovaná ve Větě o linearitě. Pro integrál neexistuje součinové pravidlo, podílové pravidlo, ani pravidlo pro složenou funkci! Protože většina funkcí je poskládána právě pomocí součinu, podílu a kompozice, znamená to, že je nebudeme umět přímo integrovat.

Existují speciální pravidla, která pomohou se specifickými typy integrálů. To není tak dobrá zpráva, jak to zní, protože to znamená, že se procedura stává dost divokou. U daného integrálu je třeba uhodnout, který postup aplikovat, často se musí použít triky - někdy jednoduché, někdy velmi složité. I u jednoduché funkce může její integrace klidně zabrat několik stran. Neexistují žádné algoritmy, které by poradily, co dělat dál, jediným průvodcem je zkušenost. Pokud se chcete stát úspěšným integrátorem, spousta cvičení je zásadní. Na tento problém se zaměřujeme v části Teorie - Metody integrace, kde pokrýváme jednotlivá pravidla a metody, v části Přehled metod integrace se na integraci zkoušíme dívat z praktické stránky.

Tuto sekci uzavřeme letmým pohledem na otázku integrovatelnosti. Protože integrace je dosti těžká procedura, asi nepřekvapí, že pro mnohé funkce to není vůbec možné. To je příklad skokové funkce, kterou jsme už viděli jako příklad v části o Riemannově integrálu. Tady dokážeme, že tato funkce nemá na intervalu ⟨0,2⟩ primitivní funkci.

Dobrá zpráva je tohle:

Věta.
Jestliže f je spojitá funkce na uzavřeném intervalu I, pak tam má primitivní funkci.

Bohužel, tato věta zas není až tak dobrá, jak vypadá. Předně, věta sice říká, že primitivní funkce existuje, ale ne jak ji najít (to je vlastně pro matiku typické). Co je horšího, ta slíbená primitivní funkce může být jen teoretická, čímž teď míníme, že existuje a dá se nakreslit její graf, ale ten graf je tak zvláštní, že se jeho tvar nedá popsat žádnou algebraickou kombinací elementárních funkcí.

To je zrovna příklad funkce

To je velice pěkná funkce zadaná jednoduchou formulkou, spojitá na celé reálné ose. Vlastně je to slavná zvonovitá křivka či Gaussova křivka, hodně používaná v pravděpodobnosti:

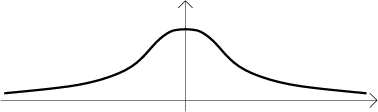
Podle věty má primitivní funkci, na obrázku vidíme jednu z nich:

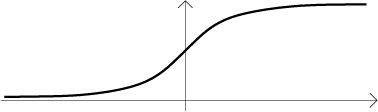
Tento tvar ale nejde popsat použitím elementárních funkcí. Ať už si jako F vymyslíte jakoukoliv formulku, nikdy nedostanete F ′ = f. Takže ačkoliv je tato funkce velice pěkná a jednoduchá, její primitivní funkci nedokážeme napsat.

Takových funkcí je víc, několik hezčích si vypíšeme. Všechny následující integrály existují, ale primitivní funkce nelze zapsat pomocí elementárních funkcí:

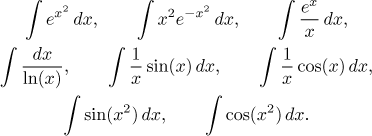
Tyhle se také hodí zapamatovat - alespoň člověk hned ví, že to má vzdát. Alespoň pro teď. Jejich primitivní funkce se totiž dají zapsat pomocí mocninných řad, ale to už je látka ze zcela jiné části, viz Aplikace řad v části Řady - teorie - Řady funkcí nebo tento příklad v části Integrály - Řešené příklady - Integrály.

Základní věta integrálního počtu
Zpět na Teorie - Úvod do integrace