Properties of the Riemann integral
We start by listing some properties that should seem obvious because the
Riemann integral is understood as an area (mathematical).
Fact.
(i) Let f be a Riemann integrable function on
[a,b].
If f ≥ 0 on [a,b], then
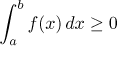 .
.
If f is continuous on [a,b] and
f > 0 on [a,b], then
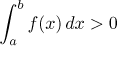 .
.
(ii) Let f be a Riemann integrable function on
[−a,a].
If f is an odd function, then
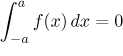 .
.
If f is an even function, then
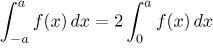 .
.
(iii) Let f be a Riemann integrable function on
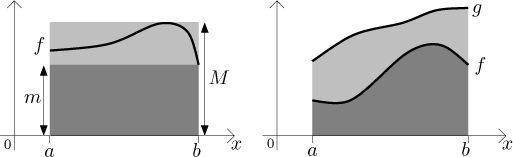
[a,b]. If m,M are real numbers such
that m ≤ f ≤ M
on [a,b], then
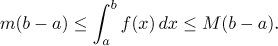
(iv) Let f and g be Riemann integrable functions on
[a,b]. If
f ≤ g
on [a,b], then
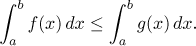
(v) Let f be a Riemann integrable function on
[a,b]. Then its absolute value
| f | is a Riemann integrable function on
[a,b] and
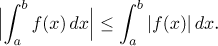
The two properties in (ii) follow from the symmetry of graph just by looking
at a picture:
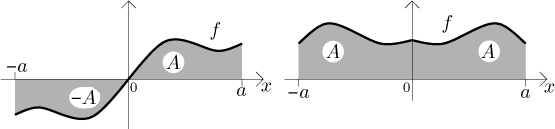
Also other kinds of symmetry can be useful at times, for instance the
following result should be hardly surprising:
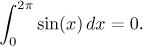
Indeed, since the graph of the sine function is symmetric,
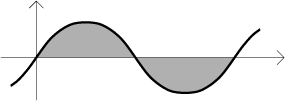
the areas above and below the x-axis cancel each other out.
The comparison properties (iii) and (iv) should be clear from this picture:
While the above facts were basically just observations, the following
properties are quite important:
Theorem.
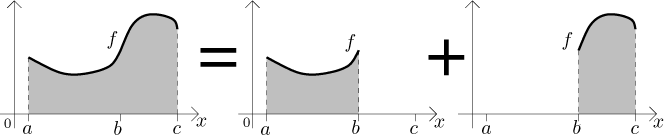
(i) Let a < b<c be real
numbers, let f be a function defined on the interval
[a,c]. The function f is Riemann
integrable on [a,c] if and only if it is Riemann integrable on
both [a,b] and [b,c];
then also
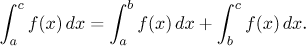
(ii) Let f be a Riemann integrable function on
[a,b], let k be a
real number. Then the function kf is Riemann integrable on
[a,b] and
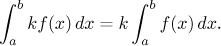
(iii) Let f and g be Riemann integrable functions on
[a,b]. Then the function
f + g is Riemann integrable on
[a,b] and
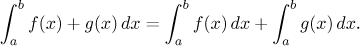
The first property should be again clear from a picture:
The second property follows algebraically from the definition of the Riemann
integral. Indeed, the constant k can be factored out of the supremum
and infimum of f over individual segments, then out of the sums for
upper and lower limits and finally from the infima and suprema defining the
integral.
The third property is less obvious, since the supremum of a sum of two
functions is definitely not equal to the sum of individual suprema. However,
one has a suitable inequality there and it can be worked out. There is also a
geometric argument, a curious reader may find the outline (along with some
interesting tidbits concerning areas)
here.
Newton integral
Back to Theory - Introduction
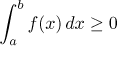 .
.
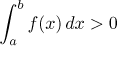 .
.
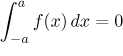 .
.
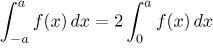 .
.
![]()
![]()
![]()



