Definition.
Let f have an antiderivative F on an interval I,
where I is an
interval od arbitrary type from a to b. We then define the Newton definite
integral of f from a to b by
![]()
If the limits exist finite, we say that the integral converges.
The fact that many functions are not Riemann integrable inspired development of different kinds of definite integrals. Today this represents a vast body of knowledge. Here we will just briefly outline two popular and intuitively simple definitions of definite integrals.
Definition.
Let f have an antiderivative F on an interval I, where I is an interval od arbitrary type from a to b. We then define the Newton definite integral of f from a to b by
If the limits exist finite, we say that the integral converges.
This definition is done in this general way so that it can be also applied to other intervals than closed ones, it will even apply to intervals whose endpoints may be infinite, in which case we actually obtain the improper integral (cf. here).
At this moment, the most natural setting is when F is an
antiderivative of f on
![]()
From the Fundamental Theorem of Calculus we immediately get the following:
Corollary.
If f is Riemann integrable and Newton integrable on[a,b], then the two definite integrals agree.
Indeed, we then have exactly the Newton-Leibniz formula.
Note that in general, these two notions need not agree. The example of jump function shows that there are functions that are Riemann integrable without being Newton integrable. There are also examples of functions that are Newton integrable without being Riemann integrable.
We will not present a precise definition here, because this would involve some fairly advanced mathematics. We will just try to show the main idea.
When we defined the Riemann integral of a function f, we split the area under the graph of f into vertical strips given by partitioning the x-axis. The Lagrange integral does it in a different way: it splits the area into vertical strips given by partitioning the y-axis.
Choose some value y and consider a very thin horizontal slice at the
level of y. If it intersects the graph of f, look at the set
B of all points x such that
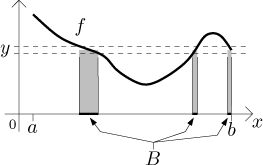
Now consider the region under the parts of the graph of f that lie in
this strip (the shaded area). If we can somehow find a way to measure the
size of the set B, then the area of the shaded part is equal to
y times the size of B. There are many ways to measure the size
of a set. The Lebesgue integral uses one that is called Lebesgue
measure and is too difficult to describe here. The Lebesgue measure is
quite natural, for instance, the Lebesgue measure of an interval
The set measuring is the main problem of this approach. If the function is very wild, the set B can be very strange and we may have no way of measuring its size. However, the Lebesgue measure is very powerful and if the function is remotely nice, we can measure sets corresponding to all values of y. Note that if the horizontal strip at level y does not cross the graph of f, the corresponding set B is empty and has measure zero.
From the picture it would seem that if you consider those shaded regions as above for different values of y, the regions are disjoint:
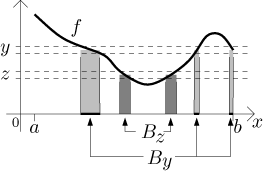
Therefore, the total area under the graph is the sum of areas of all of these regions:
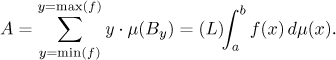
This is called the Lebesgue integral of f.
Since the definition is very complicated, one can expect that the notion of Lebesgue integral is very powerful. Indeed, it can be applied to some very strange functions, even to the Dirichlet function that is not Riemann nor Newton integrable. One can prove that the Lebesgue integral of this function over any interval is equal to zero. Using the Lebesgue integral we can also integrate over other sets than just intervals.
In order to make sense, new notions of integrals should not conflict with the accepted ones. Indeed, for "nice" functions, the value of their Lebesgue integral agrees with the Riemann and Newton definite integrals. For instance, if f is continuous, then it is integrable in all ways and
![]()