Introduction to improper integrals

When we defined the definite (Riemann) integral on a closed interval I, we had two basic conditions on the integrated function: We wanted it to be defined and bounded on the whole interval I. (We recall that these two conditions do not yet guarantee that such a function is Riemann integrable).

Now we will try to extend this definition to more general cases. Essentially, two things can go wrong. First, one or both endpoints of I can be infinity (then we naturally cannot have a closed interval), another problem may be that the function is not defined or bounded on I. The easiest case to handle is when something bad happens at one of the endpoints of I. In the following definition we will handle the situation when the right endpoint is suspect:

Definition.
Let a be a real number, let b > a be a real number or b = ∞. Let f be a function that is Riemann integrable on intervals [a,B] for all B from (a,b). We then define the improper Riemann integral of f from a to b by

assuming that the limit converges. We then say that the improper integral converges.

If the limit does not converge, we say that this improper integral diverges.

To understand the meaning of this definition, we will look at two typical examples of "bad right endpoints". In the first picture, the function "blows up" at b, in the second example we have an interval going to infinity:

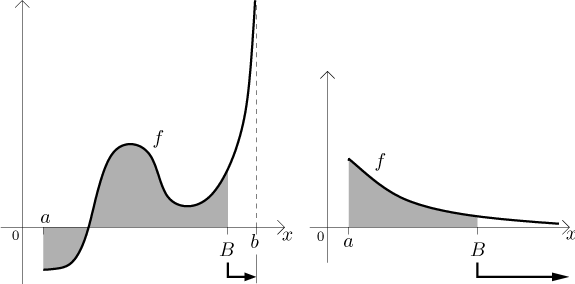
In each case we can avoid the "bad end" by cutting it away - we can use some cutoff point B for it. On the interval [a,B] we can integrate (this is the assumption of our definition), we can therefore determine the area under the graph of f from a to B. If we want to get some idea about the area under the graph of f all the way to b, the natural approach is to take the areas that we obtained for different B's and ask what happens to them when we let B get really close to b. This, of course, means limit, and we have to approach b from the left, otherwise the "badness" of f would be included in our areas and the whole procedure breaks down.

Note that when evaluating definite integrals, we prefer to use antiderivatives. In other words, the assumption on Riemann integrability in the definition is good enough for theory, but we would really appreciate if the function also satisfied assumptions of the Fundamental Theorem of Calculus. The natural thing to ask for is that f is continuous on all intervals [a,B], which means that it should be continuous on [a,b).

We can also have a "problem" at the left end:

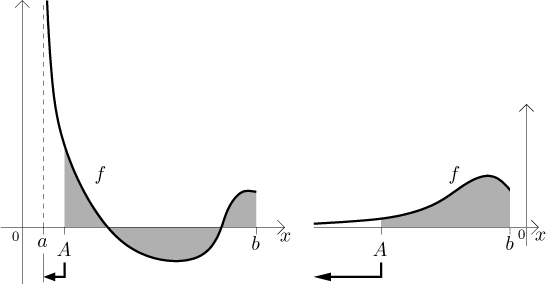
The appropriate definition is now clear:

Definition.
Let a be a real number or a = −∞, let b > a be a real number. Let f be a function that is Riemann integrable on intervals [A,b] for all A from (a,b). We then define the improper Riemann integral of f from a to b by

assuming that the limit converges. We then say that the improper integral converges.

If the limit does not converge, we say that this improper integral diverges.

Again, we usually do not use the assumption as written but try for something more; in this case we would want f to be continuous on (a,b], then the Riemann integrability on all [A,b] follows and the corresponding definite integrals can be evaluated using antiderivatives.

These two definitions show exactly how to evaluate improper integrals of this basic type, there is no special method needed.

Example: Evaluate (if it converges)

Here clearly the trouble is at infinity, the upper limit. If we integrate only up to some number (greater than 1), the function is continuous and hence Riemann integrable, there are no other troubles. Thus we can use the first definition:

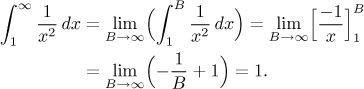
The integral converges.

Note that it means the following: If we look at the graph of this function,

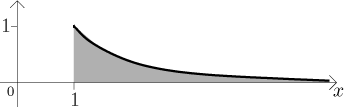
we see that the region under it is not bounded, it keeps going to the right without ever ending. Yet, it has a finite area. The reason for this is that the graph approaches the x-axis really fast, so that the increases in area as we go further to the right do not add up to infinity (or, as we saw, not even to a large number). This is related to the fact that if numbers keep getting small fast enough, we can add infinitely many of them and get a reasonable answer (cf. geometric series).

However, functions that do not tend to zero at infinity fast enough may have an infinite area (in other words, such an integral would diverge). Just drawing a picture should convince you that if you take a positive function that converges to a non-zero number (or infinity) at infinity, the integral to infinity must be divergent (as the area should clearly be infinite). Therefore, for instance,

We had an example of a convergent integral. To see what can go wrong and cause an integral to diverge, look here.

An important remark: What happens if we use this procedure on a proper Riemann integral? That is, what if f is Riemann integrable on a closed interval I and we apply the above "cut-off and limit" procedure to one of its ends? We get the correct answer. This follows from the theorem on limit properties of the Riemann integral. It therefore follows that this definition of improper integral generalizes the usual Riemann integral.

Now we will define a more general case, the generalized Riemann integral. Here we will assume that we are trying to integrate a function f over some interval I and there are some "bad places" that do not fit the above basic situations, that is, there is more than one such place and/or there is some problem that is not at one of the ends of I.

Since a definite integral should be additive (the area of a disjoint union of regions should be the sum of individual areas), we simply split the integral into several "smaller" ones, each of which will have just one "problem" in it, namely at some endpoint. In the following picture, there are three problems: at points b, d, and at infinity. To have just one problem in each smaller integral, we need to pick some dividing points (here c and e) and consider five integrals, each of which has just one problem at some endpoint. Thus they can be evaluated using the above basic definitions:

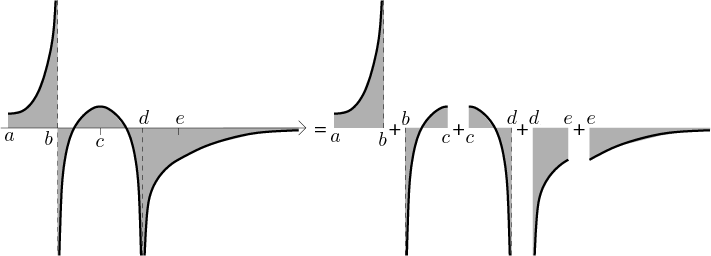
Formally:

An integral that exists may converge or be infinity or minus infinity. It does not exist if in the decomposition as in the definition we arrive at the indeterminate expression ∞ − ∞, which essentially says that the area we investigate has both infinite part above the x-axis and also below and nothing reasonable can be said about it.
To put it another way, an integral that diverges may diverge nicely (when the area is infinity or minus infinity, which is not nice but still tells us something), or badly (when there are opposing infinities mixed up in the area).

Again, this definition tells us how to evaluate generalized Riemann integrals.

Example: Evaluate (if it converges)

We can see that there are two problems, namely when x = 1 (then we divide by zero, hence the function is not bounded around 1 and also not defined at 1) and when x = ∞. We therefore need to split the interval [0,∞) into several pieces. We can start at 0 (no problem there) and go all the way to 1 - we obtain an improper integral with a problem at the right end. We cannot continue from 1 all the way to ∞ as this integral would have two problems. So we split it into two parts at some number that we choose arbitrarily, as long as it is greater than 1. For instance, we can try 5. We get

Now:

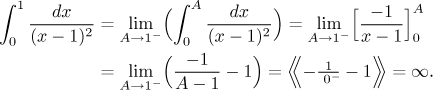
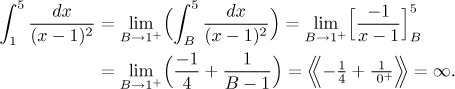
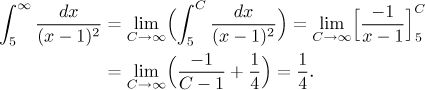
Since some of the above integrals were divergent, it follows that the integral in question also diverges. As a matter of fact, after the first integral that we evaluated did not come out convergent, we could have stopped right there and say that the whole integral from 0 to ∞ is divergent - the other two cannot fix it. But we did evaluate them and therefore we are able to say that the given integral is divergent, but in a nice way, it exists. We would write it like this:

The whole procedure can be expressed by the following picture:

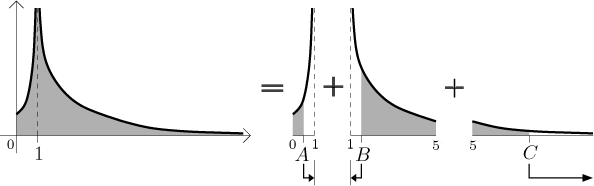
Note that the first two regions that keep going up without ending have infinite areas. It is not necessarily so for all functions with a vertical asymptote. If the graph of some function gets close to its vertical asymptote faster than the one in our example (if it "hugs it" more), the unbounded region could well have a finite area. We refer to examples in the next section.

It should be noted that here we again evaluate the smaller integrals via antiderivatives, hence our observation from the first part concerning continuity (as the easiest way to the Fundamental Theorem of Calculus) is still valid. Therefore, when we are given an integral from a to b, we always scan this closed interval for problems of two kinds: points where f is not defined and points where it is not continuous. Recall that a continuous function on a bounded closed interval must be bounded (see Continuity in Functions - Theory - Real functions). This means that when we scan for continuity problems, we also cover in this way all problems concerning boundedness of f. Thus by scanning for definition and continuity problems we cover all possible problems; in other words, it is mathematically correct.

Important Remark: The evaluation of improper integrals via antiderivatives involves a possible trap. Many antiderivatives are found using methods that yield a result in the form of a sum of terms. It is vital that when we do the limit procedure, we apply the limit to the whole antiderivative. If we fail to do this, we may end up with an indeterminate expression, although the improper integral in question may be convergent.

Consider the following example: Let f (x) = 0 be the constant zero function. Since there is no area under its graph, the integral of f from 0 to infinity should be convergent (and equal to zero). Now we try to find an antiderivative to f in a way which is perhaps unusual, but mathematically correct:

The trouble comes when we try to use this antiderivative in the improper integral from 0 to infinity and yield to the temptation of splitting the limit into two:

We got a difference of two infinities, which is an indeterminate expression. Since the limits are divergent, one is tempted to claim that the improper integral is divergent. This would be a wrong conclusion. The infinity in our result is not a part of the problem (area under the graph of f ), merely a product of our clumsy handling of the antiderivative. If we did not split the result into two limits, there would be no infinity:

You probably feel that you would never make such an obvious mistake as we did above, but the same problem can happen for instance when integrating using the partial fractions decomposition; it may then seem natural to apply the limit to each partial fraction separately, which could lead to the same trouble as above. It is therefore crucial to always keep the antiderivative together and apply the limit to the whole expression.

Note that this problem is fundamentally different from the procedure of splitting an integral into smaller ones which we used above to ensure that there is just one problem in each integral. In that case we did a procedure which corresponds to geometric splitting a region into smaller parts. If we then find that one of the parts does not have a finite area, the whole region is "bad" and other parts cannot fix it. Even if there was another part with equally infinite area but with opposite sign, the infinities would not cancel; if a region is "bad" somewhere, it is simply "bad". The problem with antiderivative is something entirely different. If we express an antiderivative as a sum of terms, it has nothing to do with regions, and troubles arising by handling each part separately are of our own doing. We will try to illustrate this point in Solved Problems.

Important Convention Concerning Notation

The way we evaluate improper integrals here is not exactly convenient. If you look at examples above and successive sections, you may notice that we in fact evaluate the integrals as usual, just at the end instead of substituting we handle the problematic endpoints using limits. This leads us to the usual way of writing such calculations, we will show it on one of the integrals evaluated above.

It is markedly shorter than the evaluation exactly according to the definition, yet still correct as long as we follow the basic rules: In an integral that we evaluate in this way at most one problematic endpoint is allowed, and it must be substituted using a suitable one-sided limit. In practical parts of Math Tutor we will obviously use this convenient way, here in the part on theory we will stick to the proper way according to the definition, since it precisely captures the substance of indefinite integral, thus helping us with understanding the topic.

Properties and examples
Back to Theory - Improper Integrals