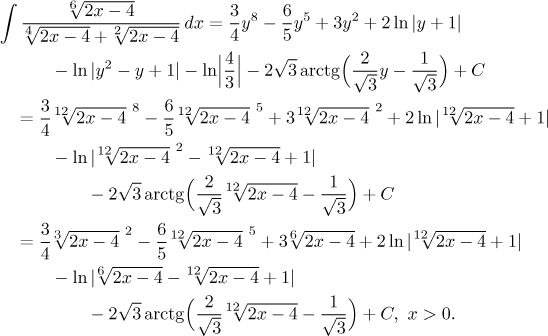Příklad: Vypočítejte integrál

Řešení: Tohle je ukázkový integrál ze šuplíku "integrály s odmocninami". Metoda říká, že se máme zbavit odmocnin tím, že substitucí místo 2x − 4 dáme vhodnou mocninu. Čím menší mocnina, tím lépe, nejmenší možná je rovna nejmenšímu společnému násobku odmocnin; v našem případě je to 12:

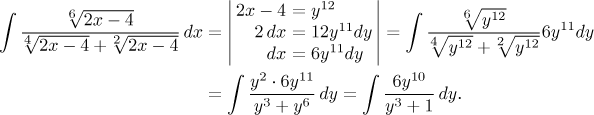
Teď nás čekají parciální zlomky, protože letmý pohled napoví, že nějaká šikovná substituce neuspěje. Nejprve musíme vydělit čitatel jmenovatelem, ve zbytku potom rozložit jmenovatel na faktory. To je obecně těžké, ale naštěstí umíme uhodnout jeden kořen y = −1. Pak uděláme rozklad na parciální zlomky.

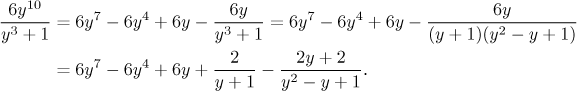
Kvadratický člen nejde dále rozložit. Konstantu u lineárního zlomku jsme získali zakrývací metodou, zbylé dvě například dosazovacím trikem. Detaily najdete zde. Můžeme tedy integrovat. První čtyři členy se integrují snadno, jen ten poslední je vyžaduje více práce. Podle algoritmu je třeba nejprve doplnit čtverec ve jmenovateli a substitucí nechat zmizet lineární část, pak rozdělit na dva zlomky a dál už je to jasné.

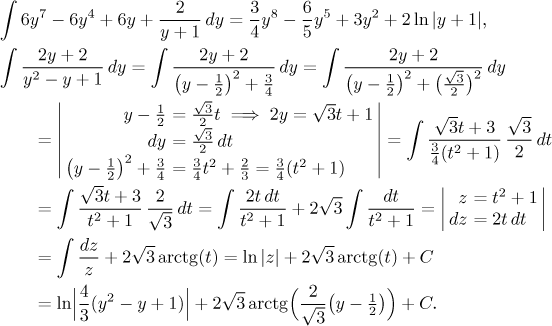
Teď to dáme dohromady a pak se udělá zpětná substituce. Jeden zaznamenání hodny krok je oddělení čísla 4/3 z logaritmu a schování do konstanty C.

Další příklad
Zpět na Řešené příklady - Integrace