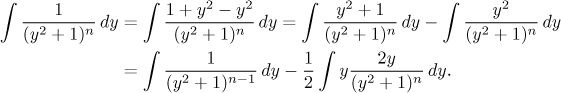
Zde odvodíme redukční vzorec pro integrování parciálních zlomků s mocninou kvadratického členu. Nejprve je nutno si integrál připravit na per partes pomocí metody přičtu-odečtu:
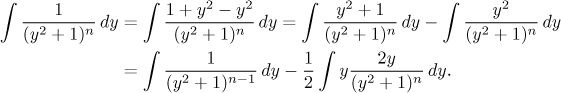
První integrál necháme, jak je, na druhý použijeme metodu per partes:
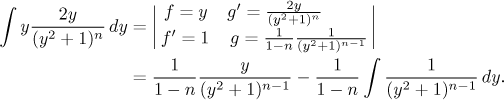
Mimochodem, funkce g byla nalezena pomocí substituce
Když teď dosadíme, dostaneme
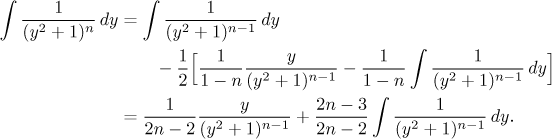
A je to. Existuje ještě jiná metoda výpočtu, kdy se daný integrál změní v jiný pomocí nepřímé substituce (viz šuplík odmocniny z kvadratických):
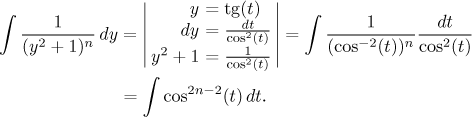
Integrál ze sudé mocniny cosinu se řeší pomocí redukčních vzorců, které se ovšem zase odvozují integrací per partes (viz tato poznámka), takže jde vlastně o stejný výpočet, tou substitucí se jen trochu zjednodušil zápis (možná).