Šuplík "integrály s odmocninami z kvadrátů"

Zde se budeme bavit o integrálech funkcí, které obsahují odmocniny (ale i mocniny) z kvadratických výrazů. Existují v zásadě tři přístupy, jak se s tím vyrovnat, a to pomocí goniometrických funkcí, pomocí hyperbolických funkcí a Eulerovými substitucemi.

Goniometrické substituce

 • Typ integrály s výrazem .

Použijte nepřímou substituci y = A⋅sin(t). Dostanete

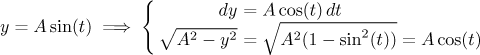
Jak vidět, odmocnina se touto substitucí odstraní. Při troše štěstí pak vzniklý integrál z goniometrických funkcí zintegrujete. Pak vás ovšem čeká převést výsledek zpět do původní proměnné (což může být někdy problém, viz níže).

Pozorný čtenář se teď ovšem může ohradit, že v představené substituci je chyba. Správně by totiž ten kosinus v druhém řádku měl být v absolutní hodnotě. V tomto konkrétním případě je to ovšem v pořádku. Funkci sin(t) uvažujeme na intervalu (popřípadě na intervalu , kdyby se například ta odmocnina objevila ve jmenovateli zlomku), vysvětlení najdete u nepřímé substituce v sekci Substituce v části Teorie - Metody integrace. Na obou uvažovaných intervalech je funkce cos(t) nezáporná, absolutní hodnoty tedy opravdu není třeba.

Příklad:

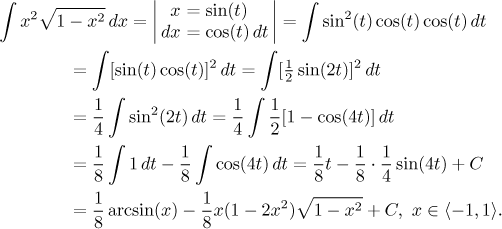
Jak se dojde k výsledku na posledním řádku? Zpětná substituce bývá u tohoto typu substitucí často dobrodružná a obecná strategie je přepsat výsledek do tvaru, který z goniometrických funkcí používá jen tu, kterou máme v substituci, v tomto případě sinus. Podrobný výpočet najdete zde.

I v příkladech u následujících substitucí se vždy budeme snažit výsledek upravit tak, aby v něm byly jen goniometrické funkce, které se objevily, když jsme tu substituci původně zaváděli. Určitou pomoc nabízí obrázky, jak je vysvětleno v poznámkách na konci části o goniometrických substitucích.

 • Typ integrály s výrazem .

Použijte nepřímou substituci y = A⋅tg(t). Dostanete

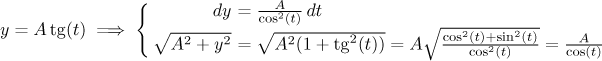
Také při této konkrétní substituci není třeba dávat absolutní hodnotu po zbavení se odmocniny; důvodem opět je, že se omezujeme na interval (popřípadě o něco menší, viz předchozí typ), kde je kosinus nezáporný.

Další postup je obdobný jako u předchozí substituce. Ukážeme si to zase na příkladě, u kterého zároveň ukážeme trik s doplněním čtverce.

Příklad:

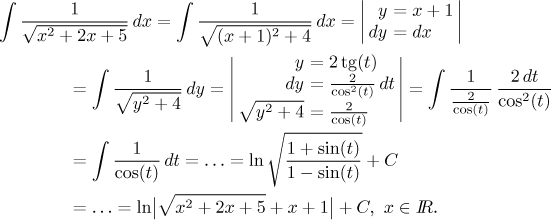
Vynechali jsme prostřední část výpočtu, protože zde nás hlavně zajímá proces zbavení se odmocniny, navíc onen výpočet integrálu reciprokého kosinu už jsme dělali v sekci o goniometrických integrálech. Opravdu zajímavý je poslední krok, kdy děláme zpětnou substituci, a tam je to drobet černá magie, protože je třeba ve výsledku vyrobit tangensy, šel by také výraz 1/cos(t), protože jej naše substituce umí nahradit. Obě vynechané části výpočtu lze vidět zde. Použije se přitom trik, který je při práci s goniometrickými funkcemi docela populární, proto doporučujem se na něj podívat.

Protože zde byla substituce tak obtížná, je načase mluvit o alternativách. Nejjednodušší způsob funguje přes trojúhelníky. Přepišme si substituci takto: tg(t = y/2. Toto lze přirozeně interpretovat jako vztah v pravoúhlém trojúhelníku, který má jeden úhel roven t a příslušný poměr odvěsen je y/2. Takových trojúhelníků je nekonečně mnoho, ale jeden mezi nimi je nejpřirozenější, a to je právě trojúhelník s odvěsnami y a 2.

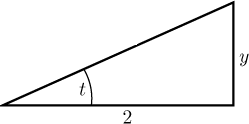
Teď jen dopočítáme třetí stranu a vyjádříme si další goniometrické funkce.

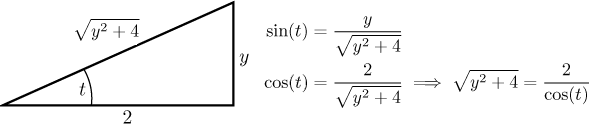
S těmito vzorci se teď dělá zpětná substituce mnohem snáze. Všimněte si, že tento trojúhelník umí pomoci i se samotnou substitucí, protože hned dává ten správný výraz pro odmocninu, které jsme se snažili zbavit.

Je tu ještě jedno velice užitečné zjednodušení. Zkušený integrátor by obě substituce zkombinoval do jedné takto:

Odteď to tak budeme dělat.

 • Typ integrály s výrazem .

Použijte nepřímou substituci y = A/cos(t). Dostanete

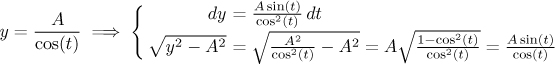
Bohužel zde to s absolutní hodnotou není tak jednoduché. Správně bychom měli integrál počítat dvakrát, jednou pro y ≥ A a podruhé pro y ≤ −A, kde v případě záporného y dostáváme tg(t) záporný, takže je třeba při odstraňování odmocniny výše použít absolutní hodnotu neboli znaménko mínus (viz tato poznámka).

Většinou ale nakonec oba výpočty vedou na stejné vzorce, takže se vyplatí nejprve spočítat verzi s kladným y a pak derivováním vyzkoušet, jestli náhodou neplatí i pro druhý interval pro y.

Příklad:

Máme použít substituci x = 2/cos(t). Přepíšeme ji jako cos(t) = 2/x, vymyslíme příslušný trojúhelník a doplníme jeho třetí stranu. Pak to použijeme k odvození užitečných vzorců, zejména výrazu pro odmocninu z integrálu.

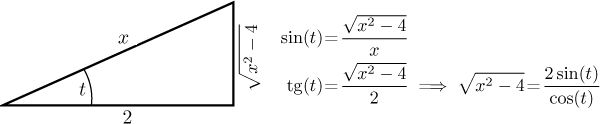
Teď jsme připraveni.

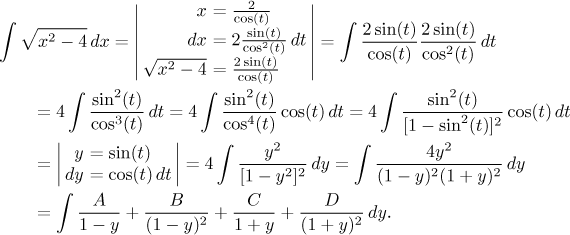
Dostali jsme parciální zlomky. Na určení konstant použijte oblíbenou metodu. Zde doporučíme zakrývací metodu k určení B = 1 a D = 1; pak získejte dvě rovnice a z nich A = 1 a C = −1. Takže pokračujeme (pozor na integrály s výrazem 1 − y, které se řeší substitucí z = 1 − y, takže dojde ke změně znaménka). Nakonec se dělá zpětná substituce, u které výrazně pomohou vzorce z trojúhelníka výše, ale vyplatí se nejprve výsledek trochu upravit.

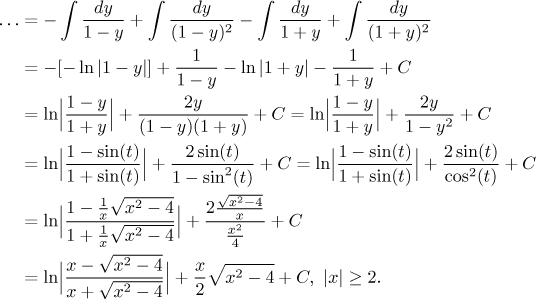
Protože jsme nepoužívali absolutní hodnotu, tak je výpočet formálně správný pouze pro x větší či rovno dvěma, ale zkouška ukáže, že vzorec platí i pro ta záporná x, takže je to vlastně dobře. Měli jsme štěstí.

Chcete-li vidět příklad, kde to s vynechanou absolutní honotou neprojde, zkuste "normální" příklad č. 4 ze Cvičení.

Hyperbolické substituce

Tyto nabízejí zajímavou alternativu založenou na identitě cosh²(t) − sinh²(t) = 1. Nejsou nicméně tak univerzální jako goniometrické substituce, protože pokrývají jen dva případy. Mají také podstatnou nevýhodu, zpětná substituce je ještě větší dobrodružství, pokud si dobře nerozumíte s inverzními hyperbolickými funkcemi (což většina ne).

 • Typ integrály s výrazem se řeší substitucí

Jak už bývá u substitucí v této sekci zvykem, podvod s vynechanou absolutní hodnotou projde, protože cosh(t) je všude kladný. Podíváme se znovu na příklad, který jsme již měli u tohoto typu předtím, zkusíme jej s novou substitucí.

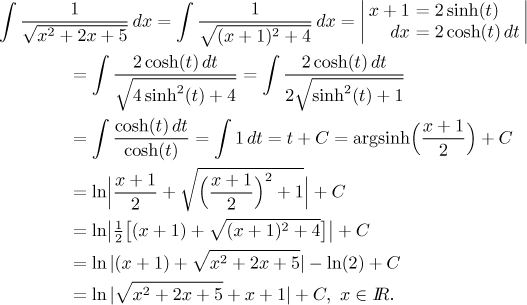
V porovnáním s naším původním řešením to vypadá jednodušeji, ale měli jsme trochu štěstí při zpětné substituci a zkopírovali jsme logaritmické vyjádření pro argsinh.

 • Typ integrály s výrazem se řeší substitucí

Zde je bohužel opět situace, kdy si formálně nemůžeme dovolit ignorovat absolutní hodnotu. Použijeme metody "doufej a bude ti pomoženo", neboli to zkusíme bez absolutní hodnoty a často zkouška vyjde. Jen v případě vážných komplikací se zkouškou bychom museli integrovat dvakrát. Zkusíme si teď tímto způsobem spočítat příklad, který jsme již měli u tohoto typu výše.

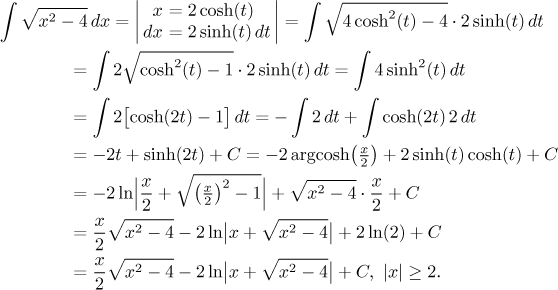
I tentokrát vypadá nové řešení zpočátku jednodušší, ale zpětná substituce je docela síla.

Eulerovy substituce

Tyto představují zcela jiný přístup k integrálům s odmocninou z kvadrátu. Kvadratický výraz se vůbec neupravuje, v závislosti na druhu polynomu se použije jedna ze tří tzv. Eulerových substitucí. Mějme tedy integrál s odmocninou (či nějakou mocninou) výrazu a⋅x² + b⋅x + c.

 • Pokud a > 0, použijeme 1. Eulerovu substituci

 • Pokud c > 0, použijeme 2. Eulerovu substituci

 • Pokud má polynom reálné kořeny u, v, použijeme 3. Eulerovu substituci

Tyto možnosti se evidentně nevylučují, takže si někdy můžeme vybrat z více možností. Všimněte si, že původní proměnná se v těch rovnostech objevuje na obou stranách, takže je třeba ty substituce nejprve přerovnat, aby se daly použít.

Vrátíme se k poslednímu příkladu, na kterém si to vyzkoušíme. V úvahu přicházejí první a třetí Eulerovy substituce. Začneme tou první, nejprve si ji připravíme.

Takže

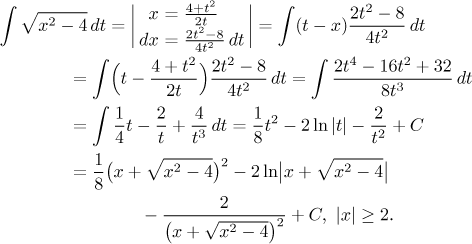
Tento výsledek souhlasí s tím, co jsme dostali předtím, jak se přesvědčíte roznásobením.

Protože je polynom pod odmocninou rozložitelný a jeden kořen je 2, můžeme použít rovněž 3. Eulerovu substituci:

a příklad se opět převede na racionální lomenou funkci. Podobně bychom mohli použít i kořene −2.

Na závěr nabídneme ještě jednu poznámku, ve které je ukázána další zvláštnost ohledně posledně předvedené substituce a zároveň zajímavá návaznost na jiný "šuplík".

Na integrály s odmocninami z kvadratik máme tedy spoustu triků. V zásadě stačí umět všechny tři triky s goniometrickou substitucí a máte pokryty všechny možnosti, nebo umět všechny tři Eulerovy substituce. V části Řešené příklady - Integrace jsou tyto postupy ukázány na tomto příkladě a tomto příkladě, mírně překvapivě také v tomto příkladě.

Zpět na Přehled metod - Metody integrace