Problem: Evaluate the integral
![]()
Solution: This integral belongs to the box "ratio of linear functions", so we use the appropriate approach. We should denote the fraction by y, but to get rid of the root we combine this trick with an indirect substitution and use y2 instead:
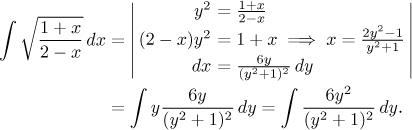
As expected, we now face partial fractions decompositions, there will be two with four constants. Since there are no linear factors, we do not get anything for free. The general method is to use multiplying out, sometimes we look for alternatives to save on calculations, but here already the multiplying method turns out to be quite simple. Details are here. We obtain
![]()
The first part is an elementary integral, for the second one we use the reduction formula:
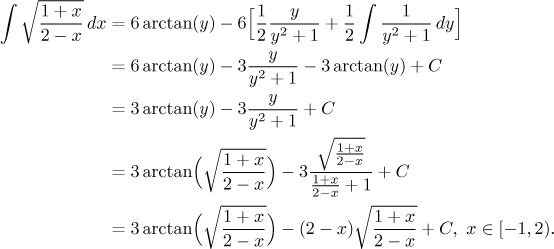
The domain of this integral is given by two conditions: The expression under the root may not be negative, and the denominator must be different from zero (however, the numerator may be equal to zero). Since we used an indirect substitution, it is vital to check the answer.
What can we do if we do not remember the reduction formula? For the square
power there is an interesting alternative, we consider it an integral from
the box
integrals with powers of
quadratics. For this quadratic expression the recommend the substitution
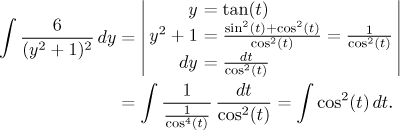
We obtained a classical integral that is easy to solve using a trig identity.
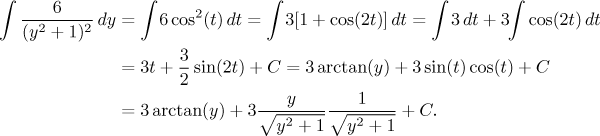
This is the same expression as we obtained using the reduction formula. As usual, the back substitution was not exactly simple and we found the appropriate formulas for sine an cosine using a suitable triangle. Note that if the power in the denominator was higher, then the new trigonometric integral would be much harder.
For this problem there is yet another interesting alternative that allows us to integrate the original rational function. It is based on the observation that by substitution we could integrate like this:
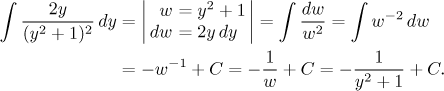
Compared to this integral, our original integral (before we decomposed it into partial fractions) has an extra y in the numerator. But we know how to get rid of extra powers: using integration by parts. The condition is that we have to be able to integrate the other half, but we just did it; so we can proceed:
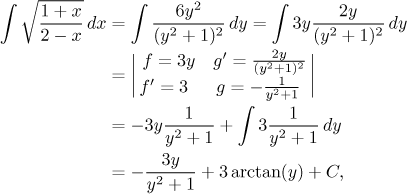
which is exactly the answer we had before.