Příklad: Rozhodněte, zda tento integrál konverguje:

Řešení: Integrovaná funkce je pro x > 0 kladná a také máme

Kdybychom se ale pokusili použít tuto nerovnost ve Srovnávacím kritériu, pomohlo by to jen v případě, že je testovací integrál divergentní. Pak by byl i daný integrál - coby větší - divergentní. Když se ale podíváme na testovací funkci, měly by nás přepadnout pochyby. Všimněte si, že pro velké hodnoty x je exponenciála mnohem větší než jakákoliv mocnina. Znamená to mimo jiné, že pak ta exponenciála ve jmenovateli bude určitě větší než x³, jinými slovy, pro velké hodnoty x,

Protože ta poslední funkce má okolo nekonečna konvergentní integrál, podle srovnání by měla mít konvergentní integrál i ta funkce nalevo. Toto podezření si potvrdíme později. Teď je jen dobré si uvědomit, že jsme pro danou funkci dostali dolní odhad, ale protože testovací integrál bohužel vypadá konvergentně, jde o situaci, kdy Srovnávací kritérium selže. Zkusíme tedy místo toho Limitní srovnávací kritérium.

Když x roste do nekonečna, v čitateli převáží x a ve jmenovateli ta exponenciála:

Teď musíme potvrdit naši volbu testovací funkce:

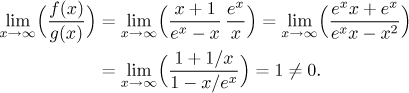
Při výpočtu jsme použili faktu, že poblíž nekonečna exponenciála přebije mocniny; přesně,

Volba testovací funkce je ověřena. Teď potřebujeme poznat, zda je testovací integrál konvergentní. Nejprve najdeme primitivní funkci pomocí integrace per partes:

Výpočet testovacího integrálu tedy vede k

Testovací integrál konverguje, takže podle Limitního srovnávacího kritéria konverguje i daný integrál.

Poznámka: Integraci per partes jsme se mohli vyhnout, pokud bychom dokázali, že existuje takové K > 0, aby pro všechna x > K platilo

Protože víme, že integrál od K do nekonečna z funkce napravo konverguje, podle Srovnávacího kritéria musí konvergovat i integrál z testovací funkce nalevo, a tedy podle Limitního srovnávacího kritéria i daný integrál konverguje.

Další příklad
Zpět na Řešené příklady - Nevlastní integrály