Příklad: Rozhodněte, zda tento integrál konverguje:

Řešení: Není vidět nějaká rozumná metoda, jak najít primitivní funkci (ověřte, že substituce a integrace per partes nezaberou). Jedinou naději tedy nabízí srovnávací testy. Protože máme přirozený odhad pro sinus, verze Srovnávacího kritéria s absolutní hodnotou se přímo nabízí. A opravdu, pro všechna x > 0 máme

Víme, že 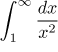konverguje, takže podle Srovnávacího kritéria konverguje i daný integrál.

Poznámky:
1. Ve většině problémů na testování konvergence nám sloužilo Limitní srovnávací kritérium jako jakási univerzální záloha. Když jednodušší Srovnávací kritérium selhalo, t Limitní pomohlo, a mohli jsme jej použít dokonce i v případech, kdy Srovnávací kritérium fungovalo. Existují nicméně problémy, kde zdánlivě neporazitelné limitní srovnání selže - a tento příklad je jedním z nich.

Co se stane, když x roste do nekonečna? Ta druhá mocnina ve jmenovateli se bude chovat jako - druhá mocnina, s tím nic nenaděláme. V čitateli máme oscilující funkci, kterou právě kvůli té oscilaci nemůžeme zrovna ignorovat. Například se můžeme pokusit porovnat danou funkci s funkcí g(x) = 1/x². Když se pokusíme to ověřit, limita

neexistuje, což ukazuje, že toto srovnání je špatně.

Podobný výpočet ukáže, že ani jiné mocniny nepomohou. Pokus se pokusíme zvýšit mocninu z 2, ověřovací limita pořád nebude existovat. Pokud zkusíme nižší mocninu, ověřovací limita vyjde nula. Například pokus g(x) = 1/x vede na

(kupříkladu Větou o sevření), takže i toto srovnání nevyšlo.

Tím se ukázalo, že mocniny coby testovací funkce nepomohou, podobný argument také vyloučí exponenciály. Závěr je, že Limitní srovnávací kritérium zde nepomůže.

2. Uvažujme problém konvergence integrálu

Ani tento nelze vypočítat přímo metodami, které známe, a Limitní srovnávací kritérium selže stejně jako v první poznámce. Zde nám ale dokonce nepomůže ani Srovnávací kritérium! Opravdu, pro x > 0 můžeme odhadovat

ale my víme, že 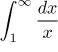diverguje, a tak není možné udělat žádný závěr.

Protože jiné testy už jsme neprobrali, tento příklad nejde vyřešit metodami, které zatím známe. Dá se to udolat trikem přes řady, viz příslušné cvičení v části Řady - Cvičení - Taylorův rozvoj.

Další příklad
Zpět na Řešené příklady - Nevlastní integrály