Příklad: Rozhodněte, zda tento integrál konverguje:
![]()
Řešení:
V tomto integrálu jsou dva problémy, jmenovitě obě meze. Nekonečno je zjevné
a
![]()
Teď se podíváme na konvergenci těchto dvou integrálů a začneme druhým. Protože to vypadá jako dost jednoduchý integrál, zkusíme jej spočítat:
![]()
(o tom posledním už víme, že diverguje). Znamená to, že nemusíme počítat ten další integrál (od 1 do 2), celý daný integrál je divergentní.
Poznámky:
1. Všimněte si, že konvergence toho integrálu, který jsme nahoře
vypočítali, nelze rozhodnout našimi testy. Nejprve zkusme srovnání. Pro
![]()
Pak také
![]()
a Srovnávací kritérium selhalo.
Mohli bychom se pokusit srovnat danou funkci s mocninami, které mají v
nekonečnu konvergentní integrál, ale to není možné. Mělo by to být vidět,
když se pokusíme o limitní srovnání. Testovací funkce
![]()
Když zkusíme ve jmenovateli vyšší mocninu, testovací funkce zase bude příliš
malá. Přesně řečeno, pro každé
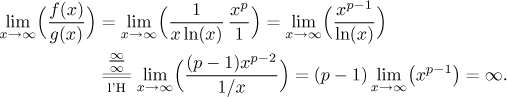
Mocniny tedy nepomohou coby testovací funkce v Limitním srovnávacím kritériu.
Teď je dobré si připomenout škálu mocnin v nekonečnu. Zatímco
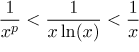 pro velká x. Tím se
vysvětluje, proč naše testy nemohly fungovat, dané funkci se povedlo
zapadnout přesně do mezery mezi divergentními a konvergentními testovacími
integrály. Můžeme to považovat za obohacení naší testovací škály. Dokonce se
dá dokázat podobným výpočtem jako u daného integrálu, že integrál
pro velká x. Tím se
vysvětluje, proč naše testy nemohly fungovat, dané funkci se povedlo
zapadnout přesně do mezery mezi divergentními a konvergentními testovacími
integrály. Můžeme to považovat za obohacení naší testovací škály. Dokonce se
dá dokázat podobným výpočtem jako u daného integrálu, že integrál
![]()
konverguje přesně tehdy, když
2. I když nebylo k vyřešení příkladu nutné prozkoumávat integrál z 1 do 2, je to nicméně dobré cvičení. Protože snadno integrujeme, provedeme přímý výpočet:
![]()
Takže tento integrál také diverguje. Okolo 1 se ale logaritmus chová úplně
jinak než kolem nekonečna. Například okolo nekonečna nelze logaritmus
porovnat s žádnou mocninou (jak jsme viděli v předchozí poznámce), zatímco
pro hodnoty x blízké k 1 máme
![]()
Teď už ověření vyjde:
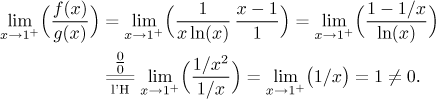
Protože testovací integrál
![]()
diverguje, podle Limitního srovnávacího kritéria diverguje také integrál z f od 1 do 2.