Theorem (Comparison test).
Let b be a real number or
If 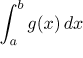 converges, then also
converges, then also
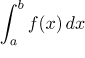 converges.
converges.
If 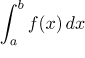 diverges, then also
diverges, then also
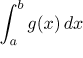 diverges.
diverges.
Quite often we do not really care for the precise value of an integral, we just need to know whether it converges or not. Since most integrals are rather difficult to evaluate, usually it is easier to just compare the integrated function to another, easier function, and then use this comparison to reach some conclusion. In this section we will only consider basic improper integrals - that is, with one "problem". More general integrals are always evaluated by splitting them into several basic integrals (with one problem), to each we then apply convergence tests. Because of the symmetry of the situation, we will state our comparison theorems for the case when the problem appears at the right endpoint.
First we will assume that the functions involved are positive. This greatly simplifies our situation. As we observed before, there are only two alternatives in this case: Either the area under the graph is finite or it is infinite.
Theorem (Comparison test).
Let b be a real number orb = ∞, leta < b. Let f and g be functions that are continuous and non-negative on[a,b) andf ≤ g on[a,b). If
converges, then also
converges.
If
diverges, then also
diverges.
The idea of this test should be clear from the picture:
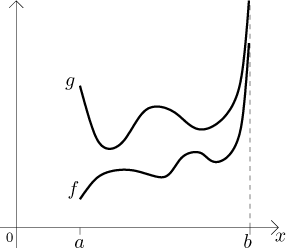
If the area under the graph of g is finite, then so should be the smaller area under the graph of f. Conversely, if the region under the graph of f has infinite area, then the larger region under the graph of g should have it, too.
The picture also makes it clear that the comparison can only work in one direction and the above two implications cannot be true as equivalences. For instance, assume that the area under the graph of f is finite. Since the region under the graph of g is larger, no conclusion is possible: its area may be finite but also infinite. This is the main disadvantage of the Comparison test.
Example:
Decide whether the following integral converges:
![]()
This integral can be actually evaluated using partial fractions, but it is
easier to answer this question using the Comparison test. We note that for
positive x,
![]() .
Since the integral
.
Since the integral
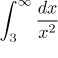 converges (this we remember, see
Properties and Examples), by the
Comparison test, also the integral in question converges.
converges (this we remember, see
Properties and Examples), by the
Comparison test, also the integral in question converges.
We just saw the main advantage of the Comparison test: very often it is very easy. This example was typical. Given a (complicated) function, we find a comparison function, typically a power, because their behaviour we know well. Then we try to establish some inequality. If we are lucky, we get the conclusion quite easily. If we are not lucky, we get to see the main disadvantage of this Test in action:
Example:
Decide whether the following integral converges:
![]()
Again, this integral can be actually evaluated using partial fractions, but
we try it using the Comparison test. We note that for positive x,
![]() .
The test integral
.
The test integral
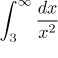 converges (as before), but this time the comparison inequality goes the wrong
way and no conclusion can be made. The Comparison test failed (as used). It
should be noted that this problem can be in fact solved using the
Comparison test, but it requires a more delicate choice of the test function
g. The justification of the inequality involved requires some work, so
in the end it is easier to use another test instead. The curious reader will
find the solution via Comparison test here.
converges (as before), but this time the comparison inequality goes the wrong
way and no conclusion can be made. The Comparison test failed (as used). It
should be noted that this problem can be in fact solved using the
Comparison test, but it requires a more delicate choice of the test function
g. The justification of the inequality involved requires some work, so
in the end it is easier to use another test instead. The curious reader will
find the solution via Comparison test here.
This example shows that it is not enough to make just some comparison. Given a function f, we try to find a suitable (simple) test function. If there is a natural candidate h that is smaller than f, it will be useful only if its integral diverges; we would look for such h if we suspected that the integral of f diverges and wanted to prove it. If there is a natural candidate g that is larger than f, it will be useful only if its integral converges; we would try to find such g if we suspected that the integral of f converges.
The Comparison test can be also thought of as a generalization of the following fact (cf. Properties of Riemann integral):
If f and g are Riemann integrable on [a,b] and
f ≤ g on[a,b] , then
The Comparison test essentially says that the same is also true for
non-negative functions and improper integrals. However, then the inequality
between integrals is not strictly true (as they might not exist), rather, it
has the following meaning: If the "smaller integral" is infinite, then the
"larger" must also naturally be infinite, since only infinity satisfies the
inequality
On the other hand, if the "larger integral" is finite, then so should be the "smaller" one, and its value must be less than or equal. This "inequality approach" also nicely illustrates why the Comparison test works one way only. We will show it by returning to our first two examples.
In the first one, we can imagine that by integrating the inequality
![]() we get the
inequality
we get the
inequality
![]()
Now it seems natural that the given integral is convergent, we even get an upper bound for its value.
In the second example, we can imagine that by integrating the inequality
![]() we get the
inequality
we get the
inequality
![]()
In this inequality, the given integral can be equal to a finite number but
also to infinity (as surely
Now it should also be clearer why we require that the function f be non-negative. If we allowed it do drop below the x-axis, we would have no control over how much area it accumulates there. Thus a comparison test for functions that change its sign a lot should involve two test functions, one that prevents f from being too large and another that prevents it for gaining too much area below the x-axis. Such a complicated test is usually not needed and we can do with an easier (but less powerful) test, a comparison test which keeps track of f by using the absolute value:
Theorem (Comparison test - an absolute value version).
Let b be a real number orb = ∞, leta < b. Let f and g be functions that are continuous on[a,b) and let| f | ≤ g on[a,b). If
converges, then also
converges.
The next test is a much stronger tool than the Comparison test. In particular, its conclusion is stated as an equivalence, so it does not share the main disadvantage of the Comparison test. Its main disadvantage is that its correct application requires more work.
Theorem (Limit Comparison test).
Let b be a real number orb = ∞, leta < b. Let f and g be functions that are continuous on[a,b), letf ≥ 0 there. Assume that the limitexists finite, but is not equal to zero. Then the integral
converges if and only if the integral
converges.
This test works in a somewhat different way. Given a function f, we
find a test function g which does not necessarily have to be greater
or smaller than f; in fact, it may sometimes go above and sometimes
drop below f. The important thing is that as x gets close to
b (from the appropriate side, i.e. from a), these two functions
should be basically equal (up to a multiple). This is verified using "limit
comparison at b", which is exactly the limit assumption in the Limit
Comparison test. In this way we justify that our guess of a test function was
correct. Typically (for the "right" guess) the limit should be equal to 1.
That would mean that when x gets close to b, the ratio
![]() is about one.
Multiplying out we get that if x is close to b, then
is about one.
Multiplying out we get that if x is close to b, then
![]()
So these integrals should come out about the same, and the conclusion of the theorem seems clear. If one of the integrals is finite, so should be the other. If one of them diverges, so should the other.
The Limit Comparison test is also true for functions that are always negative. In fact, it can be applied even to functions that do not necessarily keep their signs. But in order to work, the changes should not happen "too often". Since exact specification of this condition is not worth the trouble, people usually ignore this more general view and just use this test with non-negative functions.
Example:
Decide whether the following integral converges:
![]()
If x is close to infinity, that is, if it is a really big number, then
in the denominator the square will prevail and we can ignore the rest. This
motivates our choice of the test function:
![]()
The limit exists and is not equal to zero, so the given function and the
chosen test function are indeed very similar around infinity. Since we know
that the integral
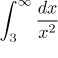 converges, it follows that also the given integral converges.
converges, it follows that also the given integral converges.
This was a typical Limit Comparison test problem. First we found a test function. Then we used limit to justify that our choice was correct. Then we looked at the corresponding integral with the test function, investigated its convergence, and finally we carried this conclusion to the given integral. For a summary of the strategy for choosing the right test function and some important examples we refer to the Methods Survey - Improper Integrals and Solved Problems - Improper Integrals.
It should be noted that the Limit Comparison test is not better (in the sense of more general) than the Comparison test. There are problems where the comparison via inequality can be achieved while the limit comparison is basically impossible. One such problem is in Solved Problems - Improper Integrals.
All three tests stated above have a companion version that handles the case when there is a problem at the left endpoint of the interval. Since the modifications are obvious, we prefer to show its application on one problem. We also use this opportunity to show how it works when the "problem" is not infinity but a vertical asymptote.
Example: Decide whether the following integral converges:
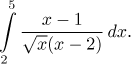
There is a problem at ![]() .
This claim has to be justified:
.
This claim has to be justified:
![]()
We see that our guess was correct as the limit yielded a non-zero number. Now we have to investigate the corresponding improper integral for our test function:
![]()
This integral is divergent, since it is one of the powers we investigated in Properties and examples and we remember it. By the Limit Comparison test, also the given integral diverges.
While the above solution followed correctly the Limit Comparison test, it may
be worth to look at the meaning of the whole procedure. The limit result in
the above comparison means that if x is really close to 2 (from the
right), then
![]() .
This implies also similarity between integrals from 2 to the right. The
square root of 2 is a multiplicative constant, so we can factor it out and
get comparison
.
This implies also similarity between integrals from 2 to the right. The
square root of 2 is a multiplicative constant, so we can factor it out and
get comparison
![]()
Since the test integral on the right is divergent and multiplication by a non-zero number cannot fix it, also the integral on the left should be divergent. We also see that the multiplicative constant we obtain during the limit comparison can be ignored in our considerations, because it cannot influence the convergence of our integrals (but it needs to be non-zero for this).
The reader now probably wonders how we came up with the test function. Indeed, this is quite difficult and requires a considerable experience, even then it can be tricky. This is the main reason why the comparison tests are mostly used for problems with infinity, respectively negative infinity. There we can imagine that x is a really big number and our intuition can help us determine which parts of the given function become unimportant.