Problem: Evaluate (if it converges)
![]()
Solution:
Both integration limits are a problem, but there are no other problems (as
![]()
Each new integral has exactly one problem which we can avoid using the cut-off and limit trick. But first we will find an antiderivative. In this integral we will use the substitution recommended for integrals with roots, which will lead to an elementary integral via a factoring trick from the arsenal of rational functions.
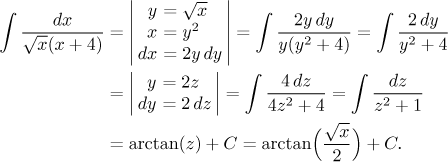
Now it is time to evaluate both integrals in the above decomposition:
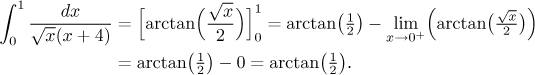
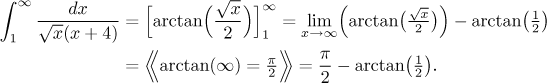
Since both integrals were convergent, the given integral is also convergent and
![]()